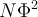Statistique : Tester l'association de variables
 Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales ( de Spearman,
de Spearman,  de Kendal), ou nominales (
de Kendal), ou nominales ( et
et  ). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
1. Tester la liaison entre deux variables
1.5. Liaison entre deux variables nominales
A.  d'indépendance (ou "Khi-deux", ou "Chi-2").
d'indépendance (ou "Khi-deux", ou "Chi-2").
Le  s'applique lorsque l'on dispose d'une table de contingence, c'est-à-dire lorsque l'on répartit les effectifs dans un tableau de
L
lignes et
C
colonnes. Par exemple, si l'on croise la variable sexe (Hommes, Femmes), avec une variable Tabagie (Non fumeur, Fumeur occasionnel, fumeur régulier), nous obtenons un tableau dans lequel chaque individu sera compté dans une seule case.
s'applique lorsque l'on dispose d'une table de contingence, c'est-à-dire lorsque l'on répartit les effectifs dans un tableau de
L
lignes et
C
colonnes. Par exemple, si l'on croise la variable sexe (Hommes, Femmes), avec une variable Tabagie (Non fumeur, Fumeur occasionnel, fumeur régulier), nous obtenons un tableau dans lequel chaque individu sera compté dans une seule case.
Nous avons vu dans le cours de L1 (section A de l'article Liaisons entre variables nominales) comment
calculer un . Nous renvoyons donc à cet article pour le détail des calculs de la valeur du
. Nous renvoyons donc à cet article pour le détail des calculs de la valeur du  proprement dite.
proprement dite.
Une fois cette valeur obtenue, on obtient le nombre de degrés de liberté tout simplement par la formule suivante :
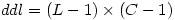
C'est le (nombre de lignes - 1) multiplié par le (nombre de colonnes - 1). Dans notre exemple précédent, cela donne (2-1)(3-1)=2.
est connue et l'on peut donc directement trouver la valeur p associée en entrant dans une table (ou avec un tableur) avec la valeur et le bon nombre de degrés de liberté.Attention toutefois au fait que la distribution du Chi-deux n'est pas symétrique et donc qu'il n'est pas légitime de travailler en unilatéral.
Précaution n°2 : la totalité des effectifs doit être incluse dans le test sous peine d'avoir des résultats biaisés. Par ailleurs, que les variables s'avèrent finalement indépendantes ou non, le test n'est valide que si les mesures sont indépendantes, ce qui n'est pas le cas si un même sujet produit des données dans plusieurs cases du tableau. Finalement, la précaution n°2 dans son ensemble se résout si l'on prend soin de vérifier que le nombre de sujets pris en compte dans l'étude est bien la somme totale des effectifs du tableau, ni plus ni moins.
B. L'indice  (phi)
(phi)
Une fois que l'on sait réaliser le test du Chi-deux, le test du Phi est presque immédiat car puisque
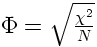
Ce qui revient à dire que
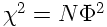
Couleur de fond
Police
Taille de police
Couleur de texte