Statistique : Tester l'association de variables
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
2. Régression linéaire simple : approche inférentielle
2.3. Récapitulatif du modèle
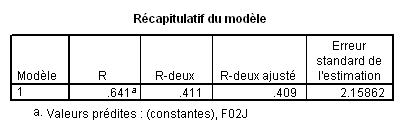
R (ou « R multiple » dans Statistica) : Il s’agit de la corrélation que l’on peut constater entre les données prédites par la droite calculée et les données réellement observées.
R traduit donc l’ajustement du modèle aux données et doit se rapprocher le plus possible de 1.
R -deux ou R² : c’est simplement le carré de R . Le carré d’une corrélation traduit la part de la variance du nuage de points expliquée par la droite de régression. Ici, la droite de régression est le modèle et R ² traduit donc la part de variance expliquée par le modèle, en l’occurrence 41,1%.
On peut aussi calculer R² directement comme part de variance expliquée par le modèle, et prendre sa racine carrée pour calculer R.
R -deux ajusté : Dans le cas général (régression multiple), c’est une valeur de R corrigée, essentiellement pour réduire un biais lié au fait que chaque prédicteur supposé peut expliquer une partie du nuage de points par le seul fait du hasard. Dans le cas de la régression simple, si n est le nombre d’observations, on a
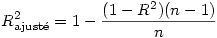
Lorsque l’on rapporte la part de variance expliquée par le modèle, mieux vaut rapporter la valeur du R ² ajusté.
Ce dernier tend vers R ² lorsque le nombre de prédicteurs est petit et lorsque le nombre d’observations devient grand. Dans SPSS et Statistica, le R²ajusté est calculé par la formule précédente mais il en existe d’autres, pour le cas où l’échantillon est petit.
Erreur standard de l’estimation : indice de dispersion des valeurs prédites. Il est égal à l’écart type des valeurs prédites divisé par la racine carrée du nombre d’observations. On utilise l’erreur standard plutôt que l’écart-type afin de pouvoir comparer des modèles ne comportant pas le même nombre d’observations.