Statistique : Tester l'association de variables
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
4. Régression linéaire multiple : coefficients multidimensionnels
4.2. Les coefficients de la régression multiple
Prenons l’exemple d’une régression à deux prédicteurs : DVP est la VD, F11VN et F02J sont les prédicteurs.
Nous obtenons :
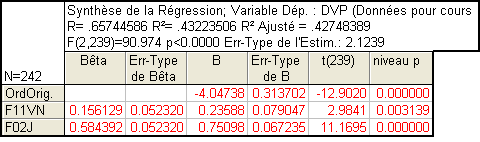
Ce tableau ressemble très fortement à celui de la régression simple mais appelle quelques commentaires.
Les B : Comme dans la régression simple, les coefficients B de la régression multilinéaire correspondent aux constantes qui définissent le poids de chaque prédicteur dans l’équation de régression.
L’équation ici est donc DVP = -4.048 + 0.236*F11VN + 0.751*F02J.
C’est l’équation du plan dans la figure vue plus haut.
Les bêtas : Comme dans la régression simple, ce sont les coefficients standardisés. On passe des β aux b par la relation
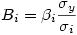
où σ y et σ i représentent les écarts-types de la VD et de la VI, respectivement.
On passe des b aux β par la relation inverse
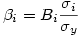
Attention :Il s’agit des écarts-types de la population et non des écarts-types corrigés (ce qui explique qu’on les note ici σ et non s).