Statistique : Tester l'association de variables
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
7. Régression linéaire multiple : Ordre d'introduction des variables
7.6. Répartition entre VIs des parts de variance expliquée
6.1. Principe général
Si l’on veut maintenant évaluer la contribution respective des différentes VI, laquelle prendre ?
Il n’y a pas une réponse unique à cette question mais eu égard aux schémas que nous avons présentés plus haut, voici ce que cela donne (il faut juste transposer le principe de ces schémas à 3VIs au cas à 4 Vis):
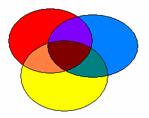
Ce schéma représente la répartition totale de la variance, que l’on cherche à connaître.
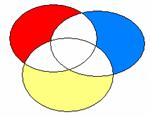
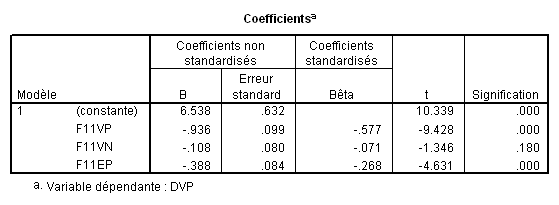
Ce schéma correspond à la méthode standard appliquée au modèle à 4 VIs. Les bêtas sont ceux du modèle 4. Si la zone bleue correspond à la part de variance attribuée à F11VP, le bêta correspondant est donc -.507. Etsi la zone rouge correspond à F02J, son bêta est .399.
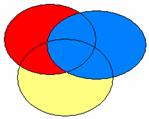
Ce schéma correspond à la méthode hiérarchique si le chercheur a mis la zone bleue dans le premier bloc, le rouge dans le second, et le jaune dans le troisième. Il correspond aussi à une méthode statistique lorsque celle-ci a conduit à la même hiérarchie des VIs.
Si la zone bleue correspond à la part de variance attribuée à F11VP, le bêta correspondant est celui qu’il possède dans le modèle 1 (-.711). Si la zone rouge correspond à la part de variance attribuée àF02J correspond à la zone rouge, son bêta est celui du modèle 2, soit .413. De façon générale, le bêta correspondant à la part de variance attribuable à une VI donnée est celui donné par le premier modèle où cette variable à été introduite (on prendra donc -.16 pour F11EP et -.128 pour F11VN).
Évidemment, toutes ces différences ne sont sensibles que si les zones d’intersection sont non vides. Autrement dit, s’il existe de la colinéarité entre les VI.
C’est pourquoi, préalablement à tout questionnement sur l’importance relative des VIs, il convient d’examiner la matrice de corrélation des VIs entre elles.
6.3. Corrélations semi-partielles
On appelle « carré de la corrélation semi-partielle d’une VI i », la réduction de R² induite par la suppression de cette VI de l’analyse. C’est donc la contribution propre de la VI au R² dans cet ensemble de VIs. On note sr i ² le carré de la corrélation semi-partielle et
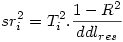
où Ti est le t de student de la i ème VI, et ddlres le nombre de degrés de liberté résiduels.
Pour illustrer cela, examinons une sortie de SPSS.
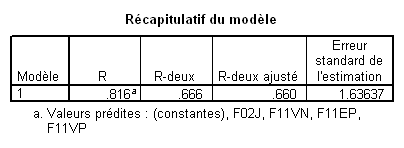
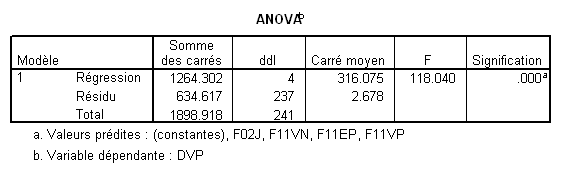
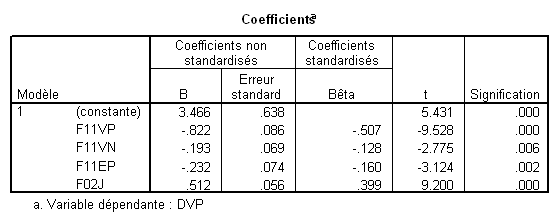
Prenons la variable F02J par exemple. Son t est 9.2, le ddl des résidus dans l’ANOVA est 237, et le R² est .666. Cela donne donc
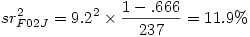
On s’attend donc à ce qu’une nouvelle analyse sans F02J donne un R² de .666 - .119= .547
Ce que nous vérifions immédiatement (aux erreurs d’arrondi près) :
Dans les méthodes hiérarchique et statistique, où toute la variance est attribuée aux prédicteurs, la somme des carrés des corrélations semi-partielles est R² .Dans la méthode standard, où la variance partagée n’est attribuée à aucune VI en propre, cette somme est inférieure à R² .
Pour terminer, signalons qu’il est possible d’obtenir directement les corrélations semi-partielles. Par exemple dans SPSS une option permet d’obtenir :
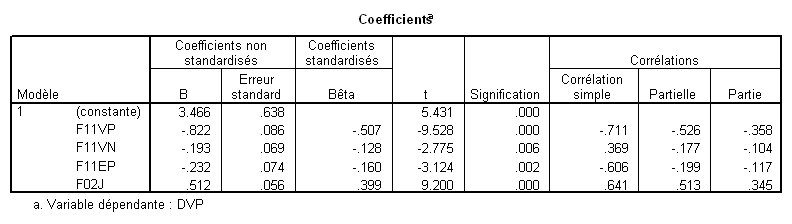
On voit apparaître la corrélation semi-partielle dans la colonne la plus à droite. Mais attention : il faut encore l’élever au carré pour pouvoir l’interpréter en termes de part de variance expliquée par le prédicteur.