UOH / Statistique et Psychométrie en L2

7.1 Test des composants de la régression (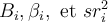$B_i, \beta_i,\text{ et } sr_i^2$)

Dans la méthode standard, le test de signification est le même pour 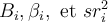$B_i, \beta_i,\text{ et } sr_i^2$.

B / Erreur standard de B

Il teste si la VI considérée explique une part significativement plus élevée de la variance de la VD, indépendamment de la variance partagée avec les autres VI. Ce qui signifie que si deux VIs sont très corrélées, l’une des deux peut se retrouver non significative. D’où l’importance pour l’évaluation globale des résultats de rapporter la matrice de corrélations complète.

Dans les méthodes hiérarchique et statistique, les tests de B_i et 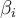$\beta_i$ restent les mêmes que ceux de la méthode standard, mais les tests de 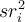$sr_i^2$ changent.

Par elle-même, la valeur de 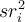$sr_i^2$ peut se calculer sur la base du fait que dans ces méthodes, la somme des 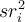$sr_i^2$ est précisément le R². Par conséquent, la différence des R² avant et après l’introduction de la ième VI donne directement le $sr_i^2$.

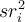Prenons comme exemple le modèle hiérarchique suivant : 

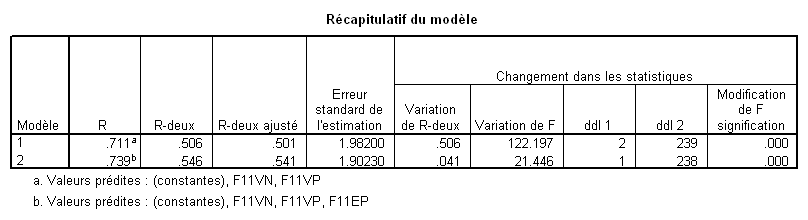
On se demande quelle part de variance ajoute F11EP dans un contexte où F11VN et F11VP ont été introduites à un niveau hiérarchique supérieur. Pour le savoir, il suffit de faire la différence des R² avant et après introduction : .546 - .506 = .04 soit 4% de variance expliquée. Cela apparaît dans la colonne « variation de R-deux ». Cette différence est-elle significative ? Oui, comme l’indique la colonne « Modification de F, signification. ».

Autrement dit, ajoute la variable F11EP dans le contexte du bloc hiérarchiquement supérieur composé par F11VN et F11VP accroît significativement le pouvoir explicatif du modèle.

7.2 Intervalles de confiance autour de B

On calcule l’intervalle de confiance d’un paramètre pour estimer sa valeur dans la population parente à partir de sa valeur observée dans l’échantillon et d’un risque que l’on accepte de prendre. Si l’intervalle de confiance contient la valeur 0, on accepte alors l’hypothèse nulle (absence de liaison dans la population parente).

Les bornes de l’intervalle de confiance sont données par l’équation :

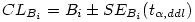
La valeur de t à utiliser est donnée par la loi de Student inverse qui prend deux paramètres, le risque α et le nombre de degrés de libertés, soit n -2.

Reprenons l’exemple où F11VN et F02J sont pris comme prédicteurs de DVP par la méthode standard. Sous SPSS, en demandant les intervalles de confiance on obtient directement : 

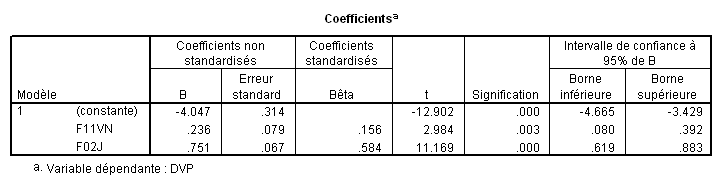
Dans notre exemple, n = 242, soit 240 ddl. Si l’on choisit comme risque α = 5%, c’est-à-dire qu’on veut que 95% des mesures tombent dans l’intervalle de confiance, la loi de student inverse pour 240 degrés de libertés et un risque de 5% donne t = 1.97.

L’intervalle de confiance de F02J est donc [.751-1.97*.067 ;.751+1.97*.067],

soit [.619 ;.883]

Ce qui signifie que dans 95% des cas, si l’on mesure la valeur de B, on trouvera une valeur comprise entre .080 et .392 pour F11VN, et entre .619 et .883 pour F02J.

Attention : ces valeurs ne sont pas comparables d’une VI à l’autre, puisque ce sont des intervalles de confiance d’un paramètre non standardisé.

Si l’on souhaite utiliser un risque α = 5%, il suffit donc de prendre les valeurs données par SPSS, et si l’on veut un autre risque, la formule est très simple à adapter. La valeur souhaitée de t s’obtient facilement sous un tableur (ici la formule était « =LOI.STUDENT.INVERSE(.05;240) »).