Statistique : Tester l'association de variables
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
8. Régression linéaire : Évaluer la qualité de la relation
8.4. Non-prédictibilité des résidus
La non-prédictibilité des résidus est l'idée qu’il ne doit pas exister de relation visible entre les résidus et les valeurs prédites de la variable dépendante.
Deux points sont à noter à ce sujet : le problème de la linéarité et celui de l'indépendance.
4.1. Linéarité et non-prédictibilité des résidus
Si on trouve une relation curvilinéaire entre les résidus et les valeurs prédites, c’est qu’il manque un prédicteur non linéaire dans le modèle. Autrement dit, d'une part le modèle manque de validité puisqu'il lui manque un prédicteur, et d'autre part l’assomption de linéarité de la relation entre VI et VD est violée. Ce constat ne remet pas en cause la capacité prédictive du modèle lui-même, telle qu'on l'a constatée, mais indique qu’il serait possible de construire un meilleur modèle en ajoutant un autre prédicteur, linéaire ou non et/ou en appliquant une transformation non linéaire à l’une des variables en jeu dans la relation.
Techniquement, on peut détecter une non-linéarité dans les résidus en sortant le diagramme de dispersion prenant comme abscisses les valeurs standardisées de la VI, et comme ordonnées les valeurs standardisées des résidus (cf. Point précédent).
Un point qu’il faut toujours avoir à l'esprit est qu’une relation non linéaire en soi, peut parfois se laisser capturer assez bien par une relation linéaire. Prenons l’exemple de la fonction Y = X ², si on se cantonne au domaine des valeurs de X prises entre 0 et 10 :
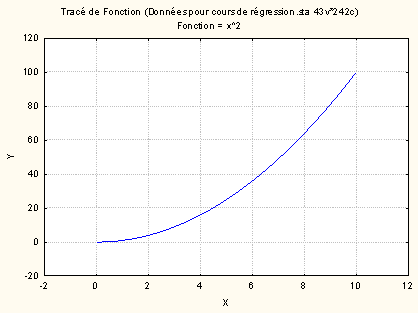
On devine sans difficulté que le nuage de points dérivé de cette fonction serait expliqué très largement par une fonction linéaire. Mais la même fonction prise entre -10 et 10 ne se laisse plus du tout ramener à une droite :
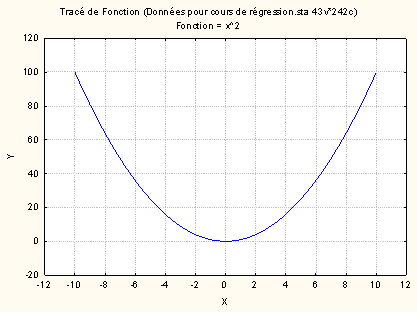
Conclusion : il faut être prudent dans l’interprétation des courbes de régression. Observer une relation d’apparence linéaire ne signifie pas nécessairement que la relation sous-jacente est véritablement linéaire. En outre, on comprend pourquoi le modèle linéaire connaît un tel succès : il peut souvent rendre compte de données qui en fait ne le concernent pas. De ce fait, si la régression linéaire est un bon outil pour mettre en évidence l’existence d’une relation, et bien qu’il puisse constituer un bon outil de prédiction, du point de vue de la production de connaissances théoriques, il vaut mieux disposer d’une approche expérimentale si l’on veut prouver quelque chose !
4.2.Indépendance
Les erreurs de prédiction doivent aussi être indépendantes les unes des autres.