Statistique descriptive
Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Rédaction : Éric Raufaste
4. Représentations graphique des distributions
4.1. La construction graphique des distributions théoriques
Attention : Pour bien comprendre cette section, il peut être utile de rappeler ce qu'est un histogramme, et savoir comment il est possible d'en construire. Rappelons qu'un histogramme est un mode de représentation graphique qui met en relation une (ou plusieurs) variables discrètes (par exemple des catégories, des classes ordinales, ou des intervalles numériques disjoints) et une variable numérique.
Une distribution est fondamentalement une représentation de la façon dont les observations (théoriques ou empiriques) se distribuent, se répartissent, sur les différentes valeurs d'une variable. Par exemple, imaginons un sociologue qui voudrait examiner les salaires des femmes en France, pour les mettre en relation, par exemple, avec le niveau d'étude. Ne pouvant accéder à l'ensemble des salaires de toutes les femmes travaillant en France, il va se rabattre, comme dans la grande majorité des recherches scientifiques, sur les salaires d'un petit échantillon de femmes. Il va s'arranger pour que cet échantillon ne soit quand même pas trop petit, et surtout qu'il soit représentatif de la population cible, à savoir la population française. Admettons donc qu'il ait bien sélectionné son échantillon, et qu'il se trouve à la tête d'un ensemble de, disons, 1000 salaires de femmes. Admettons aussi qu'il a vérifié que ses données ne contiennent pas déjà d'erreur de recueil ou de saisie. Que faire ensuite ?
La première chose à faire, c'est précisément de regarder la forme de la distribution des salaires dans son échantillon. Mais pour étudier cela, il nous faut faire un détour par un rappel un peu conceptuel de ce qu'est une distribution.
Dans le cas général, une distribution statistique théorique décrit la probabilité de trouver une valeur dans un échantillon : la surface sous la courbe représente une proportion d'observations. Par exemple, la courbe suivante décrit une distribution « normale ». On remarque que la probabilité (techniquement, on parle plutôt de « densité de probabilité ») d'avoir une observation autour de zéro est la plus forte et qu'elle décroît d'autant plus qu'on s'éloigne du zéro. Elle devient quasiment nulle très rapidement.
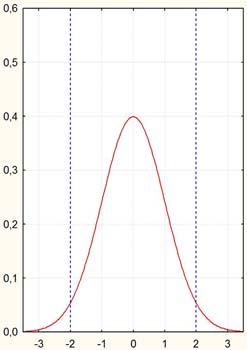
Sur la courbe de la page précédente, on voit aisément qu'il s'agit là d'une représentation graphique théorique. Par exemple, les valeurs sur les axes sont continues. Mathématiquement, cela veut dire qu'entre deux nombres, aussi rapprochés soient-ils, on peut toujours en insérer une infinité d'autres. Or dans un échantillon réel, avec des données observées donc, on ne dispose pas d'une infinité d'observations, mais toujours d'un nombre (très) limité. On ne sait donc généralement rien de la proportion d'observations qui tombent en un point donné. Il existe une infinité de points pour lesquels on ne dispose d'aucune observation, et un tout petit nombre de points pour lesquels on en a, le plus souvent, une seule. Si l'on traçait un tel graphique, on aurait quelque chose d'illisible. Dans ces conditions, comment faire ?
Il faut distinguer deux cas, selon que la variable que l'on étudie possède des valeurs discrètes ou continues. Commençons par le cas discret.