Statistique descriptive
Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Rédaction : Éric Raufaste
6. Techniques de recodage des données
6.2. Recodage par application de fonctions
Nous sommes ici dans le cas où nous avons une distribution qui n'est pas tout à fait normale alors que nous souhaitons appliquer une méthode statistique qui présuppose la normalité. Une façon simple de faire consiste à examiner la structure de la distribution et, si possible, à choisir une transformation mathématique telle qu'après l'avoir appliquée à chaque donnée, la distribution résultante ressemblera plus à une distribution normale.
Dans cette logique, la première chose à faire est de regarder le type de distribution pour pouvoir choisir la fonction mathématique adéquate.
2.1. Léger biais à gauche.
À titre d'exemple, examinons la distribution suivante, réalisée sur 1000 individus dont les valeurs sont stockées dans une variable nommée « V2 » :
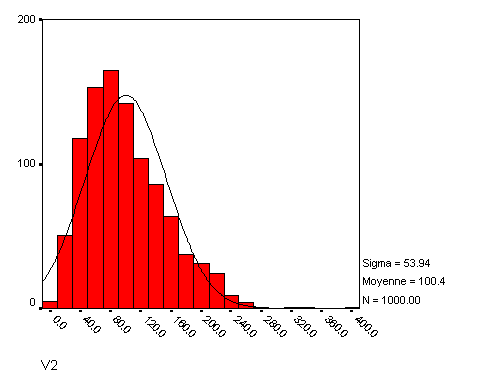
Nous voyons une forme en cloche, un peu comme une distribution normale, mais on voit aussi que l'histogramme diffère légèrement de la courbe gaussienne qui lui a été superposée. En particulier, l'histogramme semble dévié vers la gauche alors que la distribution normale est symétrique. On voit aussi qu'il existe quelques valeurs un peu perdues tout à droite alors que de telles valeurs devraient être très rares, car très éloignées de la moyenne (ici à 100 et avec un écart-type d'environ 54, cela place les valeurs extrêmes à environ 6 écarts-types de la moyenne, ce qui est considérable. D'ailleurs, si nous demandons à calculer les statistiques descriptives sous SPSS, nous obtenons un coefficient d'asymétrie de 0.90 ce qui reste acceptable, mais n'est pas parfait, et un coefficient d'aplatissement de 1.13, ce qui n'est pas très satisfaisant (idéalement la valeur absolue de l'asymétrie comme de l'aplatissement devraient rester inférieure à 1).
Sur une telle distribution, la fonction racine peut donner de bons résultats. Donc à chaque observation, on va appliquer la transformation suivante :
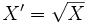
Par exemple, si la valeur de Xi était 400, la valeur de X'i sera 20. On obtient alors une variable recodée que nous allons nommer « V2R », dont voici la distribution :
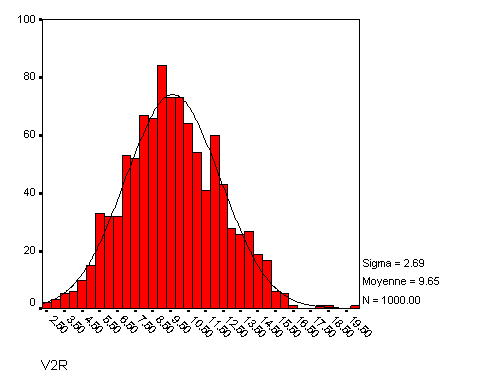
Fort logiquement, cette variable recodée varie maintenant entre 0 et autour de 20. Mais surtout, nous remarquons que l'histogramme obtenu ressemble beaucoup plus à une distribution normale, que ce soit en termes de symétrie qu'en termes d'aplatissement. Si nous demandons à SPSS de nous calculer les coefficients d'aplatissement et d'asymétrie de cette nouvelle variable, nous trouvons respectivement 0,16 et -0,16 ce qui tout à fait acceptable. À partir de là, si nous procédons à nos tests avec cette variable, les méthodes qui exigent la normalité comme condition pourront s'appliquer avec beaucoup plus de fiabilité.
Un point important est que la fonction Racine que nous avons utilisée préserve l'ordre des observations. Formellement, nous pourrons écrire que pour deux valeurs X1 et X2 positives,
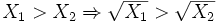
Ce point sera très important lorsqu'il s'agira d'interpréter les résultats obtenus en utilisant la variable recodée. Il faut être conscient que certaines transformations ne possèdent pas cette propriété et qu'il faut donc interpréter les résultats obtenus avec prudence.
2.2. Fort biais à gauche.
Considérons maintenant la variable V3, dont la distribution est la suivante :
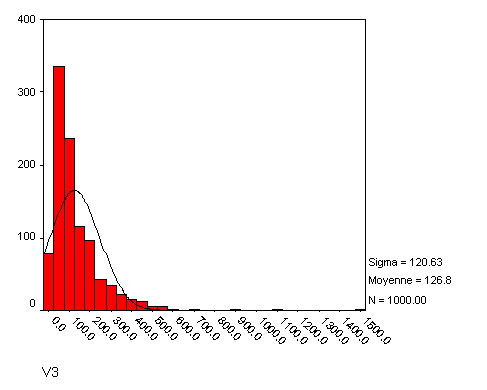
Cette fois, le biais à gauche est très marqué, probablement trop pour que l'application d'une fonction racine soit suffisante pour redresser la distribution. L'asymétrie est à 3,4, quant à l'aplatissement il s'envole à plus de 23 !! Nous pouvons cependant utiliser une autre fonction, plus appropriée à ce cas : le logarithme naturel. À chaque observation, on va appliquer la transformation suivante :
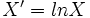
Par exemple, si la valeur de Xi était 1000, la valeur de X'i sera 6,90. On obtient alors la distribution suivante :
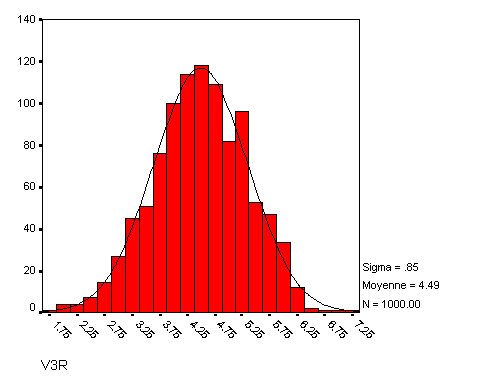
Là encore, nous avons une distribution largement plus en accord avec ce qu'on attend généralement d'une distribution dite normale. Les nouvelles valeurs d'asymétrie et de distribution que nous obtenons sont respectivement -0,11 et -0,12 ce qui est excellent. Notons que la fonction logarithme, comme la fonction racine, préserve l'ordre des observations.
Il faut cependant être conscient que ces transformations ne sont pas toujours applicables. Ainsi la fonction racine comme la fonction log ne peuvent pas s'appliquer à des valeurs négatives (vous obtiendrez une erreur si vous essayez d'appliquer ces fonctions sur des valeurs négatives). La fonction log ne peut pas s'appliquer à des valeurs nulles non plus.
2.3. Distribution en i
Dans un certain nombre de cas, la distribution sera biaisée à gauche, mais sans retomber comme dans une normale, ce qu'on appelle une courbe en i (par analogie évidente avec la forme scripte de la lettre i). En voici un exemple :
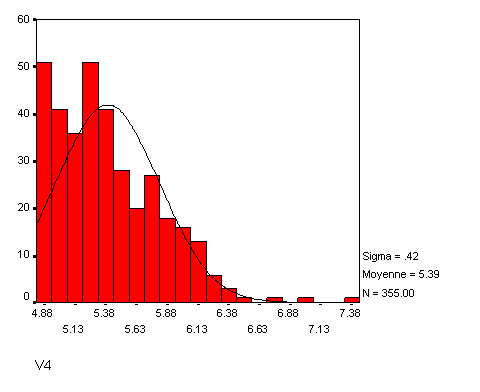
Dans ce cas, les fonctions précédentes risquent de ne pas marcher. Une solution alternative consiste alors à utiliser la fonction inverse (X' = 1/ X) peut donner des résultats satisfaisants :
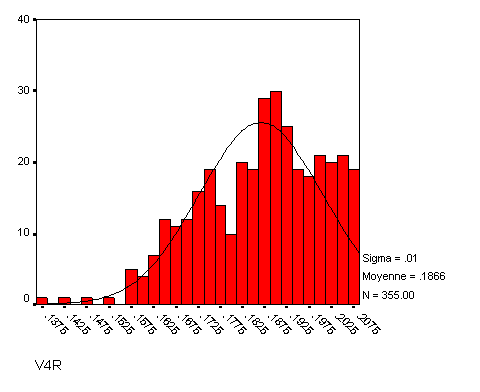
Sur cet exemple, vous pouvez avoir l'impression que le résultat n'est pas très concluant, mais si l'on demande les indices d'aplatissement et d'asymétrie, on voit qu'ils passent de 0,92 et 1,08 avant la transformation à -0,52 et -0,22 après, ce qui est clairement mieux. Cela dit, dans mon expérience en psychologie, les distributions en i et en j sont de mauvais pronostic. Souvent le caractère en i (resp. en j) résulte en effet d'un effet plancher (resp. un effet plafond), c'est-à-dire que beaucoup de sujets ayant donné la valeur la plus basse possible (resp. la plus haute), la distribution est tassée et rien ne pourra y faire, sauf à entrer dans de la cuisine plus radicale, à savoir utiliser des transformations qui ne préservent pas l'ordre des observations.
2.4. Distributions biaisées à droite
Les fonctions que nous avons évoquées précédemment s'appliquent pour corriger des biais à gauche. Que faire lorsque le biais est à droite ? Une solution très simple consiste à renverser d'abord les valeurs, afin d'obtenir une distribution biaisée à gauche, après quoi il suffit d'appliquer les méthodes précédentes.
Le renversement s'obtient très facilement en prenant la plus forte valeur de la distribution et en appliquant le complémentaire à cette valeur, soit
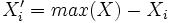
Il suffit alors d'appliquer la fonction vue précédemment, racine, log ou inverse selon les cas.