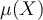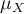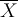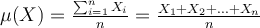Moyenne
Objectif. Définir la moyenne d'une variable quantitative.
Prérequis. Échelles de mesure, Conventions de notation (en particulier, somme algébrique)
Résumé. Soit une variable définie sur une population de N individus, on définit la moyenne de cette variable. On estime cette moyenne à l'aide de la moyenne d'un échantillon représentatif de la population.
rédaction : Éric Raufaste1. Moyenne d'une variable dans une population
Nous devrons distinguer deux cas : la valeur moyenne d'une variable dans une population (par exemple le niveau de bonheur moyen de toute la population française) et la valeur moyenne d'un échantillon restreint de la population française, échantillon sur lequel on fait la mesure (par exemple 1000 personnes) et que nous prendrons ensuite comme estimation de la valeur vraie de la population cible.
Soit une variable quantitative
X
définie sur une population de
N
individus. Par exemple,
X
prend comme valeur la taille des individus.
La moyenne de la variable X est un indice de tendance centrale qui se calcule comme la somme de toutes les observations divisée par le nombre d'observations. C'est donc une « valeur par observation » dans l'échantillon considéré.
La moyenne de la variable X, ou encore, dans le cas de la taille des individus, la taille moyenne de la population est dénotée par l'une des formes suivantes (selon les textes, on peut rencontrer les trois) :
En utilisant les conventions de notations pour les sommes algébriques, on a alors
Bien entendu, connaître exactement cette valeur supposerait de faire des mesures sur chacun des individus de la population cible. Dans le cas d'une population aussi vaste que la population française, cet objectif est hors d'atteinte la plupart du temps. Il faut donc en obtenir une estimation à partir de la moyenne observée sur un sous-ensemble de cette population, un
échantillon.
Couleur de fond
Police
Taille de police
Couleur de texte