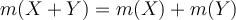UOH / Statistique et Psychométrie en L1

a. Si l'on ajoute une constante à toutes les notes d'un échantillon, la nouvelle moyenne est directement donnée en ajoutant la constante à l'ancienne moyenne, soit :

$m(X+a)=m(X)+a$

Autrement dit, si tous les individus d'une classe d'élèves améliorent leurs notes en maths de 2 points, alors la moyenne globale de la classe sera aussi augmentée de 2 points.

b. Si l'on multiplie par une constante toutes les notes d'un échantillon, la nouvelle moyenne est directement donnée en multipliant l'ancienne moyenne par la constante, soit :

$m(a.X)=a.m(X)$

Par exemple, suite à l'application d'une TVA de 19,6% sur les articles d'un magasin, (on multiplie chaque prix par 1,196) la moyenne du prix des articles après application de la TVA sera égale à la moyenne des prix avant TVA multipliée par 1,196.

c. Si l'on ajoute les notes de deux variables, observation par observation, la moyenne de la variable qui contient cette somme est égale à la somme des moyennes des deux variables d'origine, soit :

$m(X+Y)=m(X)+m(Y)$

Par exemple, si le score moyen d'intelligence d'une population s'obtient en additionnant les notes obtenues à une épreuve verbale et à une épreuve visuo-spatiale, alors la note moyenne globale obtenue sera égale à la somme des moyennes relatives à chacun des deux tests.