Calcul de la somme des carrés

1. La formule de calcul

Nous avons vu dans l'article sur l'ANOVA que la somme des carrés peut s'écrire

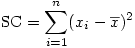
Bien qu'il ne soit pas trop difficile de voir intuitivement le sens de cette formule, il existe une autre formule du numérateur de la variance, donc de la somme des carrés. En effet, on peut montrer qu'il est équivalent d'écrire que

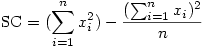
2. Pourquoi utiliser cette nouvelle formule ?

Lorsqu'on passe par une étape de calcul de la moyenne, on peut commettre une toute petite erreur d'arrondi, car les zones de calcul informatiques ne sont pas des nombres mathématiques (dont la série de décimales est potentiellement infinie) mais des espaces de stockage de taille limitée. Par exemple, si la taille de la zone de stockage permet de contenir seulement 1 nombre à trois décimales, on ne pourra pas coder la réalité du nombre Pi (3,14159...) mais seulement l'arrondi de $\pi$ à trois décimales soit 3,142. En utilisant ce nombre arrondi, on commet une petite erreur (environ 0,00041 d'excès). Cette erreur est petite mais si on utilise 10000 fois le nombre ainsi arrondi, on finit par commettre une erreur de 4,1 points ! Or, dans les gros volumes de données, il peut arriver qu'on n'utilise pas 1000 mais des millions de fois ces valeurs ! Voilà pourquoi on préfère partir d'une formule qui évite de passer par l'utilisation massive de nombres arrondis.

Mathématiquement équivalente à la formule de base, elle est aussi informatiquement plus rapide, et à mettre en œuvre. En effet, elle n'exige pas de commencer par une première étape de calcul de la moyenne du groupe.  On peut donc traiter toutes les données en une seule fois au lieu de passer une première fois pour extraire la moyenne puis une deuxième fois pour faire les différences. En cas de très gros volumes de données, c'est un avantage de temps de calcul.

C'est donc en réalité cette deuxième forme qui est mise en œuvre dans les programmes. Une fois qu'on a compris qu'il s'agit de faire le calcul pour les n lignes d'un échantillon (une colonne de données) X , on peut supprimer ces indications pour ré-écrire la formule sous une forme plus simple :

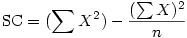
3. Total et Facteur de correction

Afin de faciliter la manipulation ultérieure des calculs, il n'est pas inutile de remarquer que l'expression précédente est en réalité composée de deux termes, un "Total" et un "facteur de correction" :

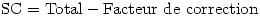
où

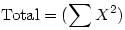
et

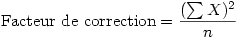
4. Exemples de calculs sur un échantillon

Voici un échantillon de données fictives où trois groupes d'étudiants ont reçu des notes entre 0 et 20. Imaginons que les trois groupes correspondent à une condition contrôle où les étudiants n'ont reçu aucun enseignement spécifique, le groupe 2 a reçu un enseignement traditionnel, et le groupe 3 a bénéficié en plus d'une auto-formation en ligne sur un site internet. Voici les données :

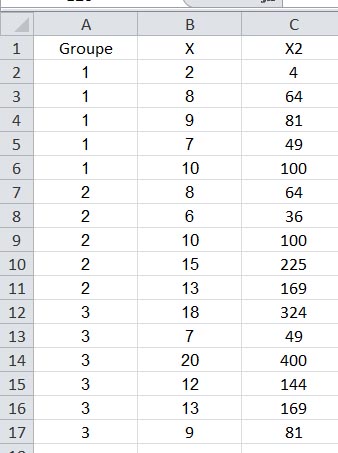
La colonne X contient les notes et la colonne X2 contient le carré de ces notes.

Nous pouvons alors, à l'aide de simples formules de tableur, calculer la somme des carrés et les degrés de libertés associés :

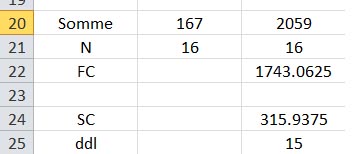
La ligne "Somme" contient la somme de toutes les valeurs, soit 167.

La ligne "N" contient le nombre de valeurs prises en compte.

La Ligne FC s'obtient selon la formule vue plus haut, soit  (167)² / 16 = 1743.0625

La somme des carrés de tout l'échantillon s'obtient en soustrayant la ligne FC de la somme des carrés, soit 2059 - 1743.0625 = 315-93.75