Statistique : comparer des moyennes

Il existe une procédure générique qui fournit des résultats généralement considérés comme acceptables. Pour en comprendre la logique, commençons par exposer l’inégalité de Bonferroni.

3.1. L’inégalité de Bonferroni

L’inégalité de Bonferroni est un théorème selon lequel la probabilité d’une conjonction d’événements A_i ne peut jamais dépasser la somme des probabilités des événements conjoints :  

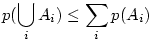
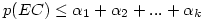
3.2. La correction de Bonferroni

Supposons que nous définissions un seuil maximum c , qui sera utilisé pour chacune de nos k comparaisons élémentaires. Puisque pour tout i , 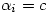, l’inégalité de Bonferroni nous dit que le risque de l’ensemble des comparaisons (EC) est

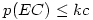
La difficulté que nous avons est que si nous opérons au moins 2 comparaisons avec un seuil de 0.05, rien n’empêche l'ensemble des comparaisons prises en bloc, "EC", d’avoir une probabilité d’erreur de type 1 supérieure au seuil de 0.5,  p (EC)>.05, ce qui n’est pas acceptable. Il faut donc prendre un seuil maximum plus bas pour les comparaisons élémentaires. Notre problème est de trouver quelle valeur prendre.

Si l'on se donne 5% comme critère acceptable pour la significativité de l'ensemble, on peut écrire que  0.05 ≤ kc , et donc 0.05/ k  ≤ c . Autrement dit, en prenant un seuil qui ne dépasse pas c/k pour les comparaisons élémentaires, on s'assure que le risque de la comparaison d'ensemble ne dépasse pas 0.05.

D’où le principe général de la correction de Bonferroni pour les comparaisons élémentaires : on applique notre test, quel qu’il soit (t de Student, ANOVA, etc…)  mais on se donne un seuil de significativité pour chaque comparaison qui soit directement dépendant du nombre global de comparaisons.

Il faut noter que cette méthode s’applique à toutes les comparaisons, et en particulier aux comparaisons planifiées (contrastes) comme aux comparaisons post-hoc. Nous verrons des exemples spécifiques dans les articles en question.

3.3. La variante de Dunn-Šidák

Il s'agit d'une légère variante du test de Bonferroni qui peut offrir un très très léger gain de la capacité à obtenir un test significatif lorsque l'hypothèse nulle est fausse (i.e, un très léger gain de puissance statistique). Le principe est le même mais on utilise l'inégalité 

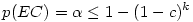
qui permet de garder l'erreur d'ensemble (EC) à un niveau inférieur au seuil α si on teste chacune des k comparaisons élémentaires au seuil 

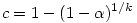
La table ci-dessous compare les seuils de signification des comparaisons élémentaires corrigés par Bonferroni et par Dunn-Šidák, afin de maintenir l'erreur de l'ensemble à un niveau .05. L'écart est minime ! De plus, le gain qu'on peut attendre décroît avec le nombre de comparaisons, et il est insignifiant quel que soit le nombre k de comparaisons si l'on veut maintenir l'erreur de l'ensemble à un niveau .01.