Statistique : comparer des moyennes
 Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
3. Comparer plus de deux moyennes : L'ANOVA à un facteur
3.3. Variations et variance dans l'ANOVA
A. La variance : formule générale classique

Nous l'avons dit, les variations sont ici mesurées par la variance, dont nous rappelons que la formule générale pour la variance
s²
d'un échantillon de mesures stockées dans une colonne de données
X
et dont la moyenne est 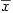 .
.
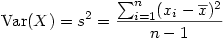
Autrement dit, si l'on suit cette formule, on va...
- pour chacune des n observations de l'échantillon que l'on considère, calculer l'écart qui existe entre cette observation et la moyenne du groupe entier,
- passer cet écart au carré puis
- faire une sorte de moyenne de tous ces écarts carrés.
J'écris ici une sorte de moyenne car pour faire une vraie moyenne il aurait fallu en diviser la somme par n alors que nous divisons par n -1 pour des raisons formelles liées au fait qu'on travaille sur un échantillon et non sur la population entière.
B. La variance n'est pas " additive "
À cet instant, il faut nous souvenir que nous cherchons à attribuer l'ensemble des variations constatées de la VD à l'une de deux sources de variations possibles : les variations dues au facteur étudié (variations inter-groupes) et celles dues à d'autres déterminants inconnus (variations intra-groupes).
Puisque dans l'ANOVA on représente les variations par la variance, nous avons donc trois types de variance :
- À l'ensemble total des variations, on pourra attribuer une variance Totale.
- À l'ensemble des variations dues au facteur, nous ferons correspondre une variance inter-groupes (on dit parfois aussi Variance du Traitement).
- Aux variations que l'on ne sait pas expliquer, nous ferons correspondre une variance d'erreur, appelée aussi, variance résiduelle ou encore variance intra-groupes.
Si l'on veut pouvoir attribuer dans nos données la part qui revient à chaque type de variation, il nous faut donc connaître la relation qui unit la variance totale, la variance d'erreur et la variance du traitement. Malheureusement, la variance n'est pas additive : dans le cas général
Var Totale ≠ (Var Traitement + Var Erreur )...
Ce n'est donc pas pratique à manipuler et c'est pourquoi, dans le détail des calculs, nous passerons par une notion légèrement différente, la notion de "Somme des Carrés".
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte

