Statistique descriptive

1.1. Généralités

C'est l'indice le plus familier, car nous l'avons rencontré maintes fois à l'école, pour évaluer nos résultats. Considérons une variable numérique, à valeurs continues (ou que l'on peut considérer comme continues compte tenu de la précision de nos instruments de mesure). Par exemple, un industriel veut doser la quantité de sucre à mettre dans une tarte, dans l'idée d'en vendre le plus possible et donc de plaire au plus de gens possible et de déplaire au moins de gens possible. Pour des raisons économiques, il ne pourra pas fabriquer plusieurs sortes de tartes. Imaginons que cet industriel a procédé à un test avec, disons, 200 personnes, et pour chacune de ces personnes, il a déterminé la quantité de sucre optimale, celle qui lui plaît le plus. Le problème est donc de trouver une valeur qui résume l'ensemble des observations de façon à ce que cette valeur minimise les écarts qui existent entre elle et les goûts des différents individus. Autrement dit, on veut la quantité de sucre pas trop grande ni trop petite, un juste milieu en quelque sorte. L'opération mathématique capable d'agréger des mesures individuelles de façon à ce que le résultat minimise la distance avec l'ensemble des observations est la moyenne. 

Rappelons simplement ici que la moyenne s'obtient en faisant la somme de chacune des observations puis en divisant par le nombre d'observations. L'étudiant qui le souhaite pourra trouver une description plus détaillée et des tutoriels (pour jamovi, R, et SPSS) dans le rappel de maths consacré à la moyenne. 

Géométriquement, calculer la moyenne correspond à trouver le milieu d'un ensemble de points. 

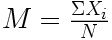
Bien que cette procédure soit optimale du point de vue de la minimisation de la distance avec les observations disponibles, il faut cependant être conscient que le résultat obtenu présente un certain nombre de défauts, et qu'il n'est pas toujours possible de le calculer.

1.2. Inconvénient 1 : absence d'existence 

Le premier de ces défauts est le fait que le résultat obtenu correspond à un nombre qui ne décrit parfaitement peut-être même pas un seul des individus sur lesquels on a procédé aux observations. Ainsi la chimère du français moyen donne un individu qui mesure exactement 1,75m, a exactement 100 de QI, etc. Cette absence d'existence devient particulièrement flagrante si l'on considère non plus des nombres continus mais des nombres entiers. On peut parfaitement calculer qu'une femme française a 1,9 enfants. Pour le premier enfant, on voit, mais à quoi peut bien ressembler le 0,9 enfant restant ? Même s'il peut-être utile à bien des égards, ce nombre est donc une chimère algébrique, mais pas une réalité physique. En même temps, c'est tout de même informatif et permet de voir que nous sommes plus proches en France du seuil de renouvellement de la population (2,1 enfants par femme, que, disons, l'Italie).

1.2. Inconvénient 2 : sensibilité aux valeurs extrêmes

Le deuxième inconvénient de la moyenne est que cet indice est très sensible aux valeurs extrêmes, c'est-à-dire que les observations qui sont très différentes de reste de l'ensemble des observations pèsent plus lourd dans le calcul de moyenne que les autres observations. Ainsi, si nous calculons la moyenne des revenus en France, les 1% de revenus les plus hauts vont peser un poids démesuré par leur caractère complètement hors de proportion avec le salaire des autres individus de la société. Et plus la société sera inégalitaire, plus le calcul du revenu moyen sera biaisé par les hauts revenus. Autrement dit, si l'on mesure la moyenne en enlevant les 1% de revenus les plus hauts, le résultat sera très différent de celui qu'on obtiendrait en incluant ces individus. Mais surtout, ce sera dans des proportions plus importantes que ce qu'on obtiendrait en retirant n'importe quel autre individu. Et finalement le résultat sera alors beaucoup plus représentatif de la réalité de la pyramide des revenus.