Statistique descriptive

Imaginons que l'on compte sur une année combien d'individus naissent chaque jour de la semaine en France. On obtient donc un nombre pour les lundis, un pour les mardis, etc. Si l'on divise ces nombres par le nombre total de naissances annuelles, on obtient ainsi pour chaque jour la probabilité qu'un individu pris au hasard naisse un lundi, un mardi, etc. Approximativement, cette probabilité sera la même pour chacun des jours de la semaine. Autrement dit la courbe obtenue ressemblera à un rectangle. C'est une distribution rectangulaire.

Bien entendu, si l'on prend un dé non pipé et qu'on regarde la probabilité que chacune des six faces sorte, on obtiendra aussi une distribution rectangulaire.

Si, maintenant, on trace le graphe des fréquences de chaque face après avoir lancé un grand nombre de fois un dé (grand échantillon), on devrait observer quelque chose qui ressemble à un rectangle, faute de quoi il sera plausible que le dé soit en réalité pipé. Voici un exemple de résultats obtenus avec 1015 lancers de dés simulés par ordinateur :

On remarque qu'il y a bien des fluctuations de fréquence d'une face à l'autre, mais celles-ci sont très petites.

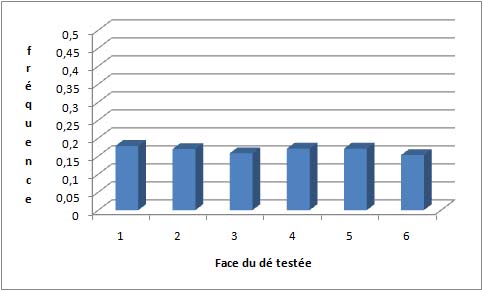
Du point de vue de la représentation graphique, vous pouvez noter que l'on n'a plus ici un axe des X avec des modalités continues, mais discrètes : on a un petit nombre de valeurs bien séparées. Cela provient du fait que nos deux exemples (lancers de dés, nombre de naissances en fonction du jour de la semaine) utilisaient des variables discrètes, c'est-à-dire dont les modalités sont bien séparées. Il n'existe pas de « lundi et demi » dans la semaine ni de « face 4,3 » sur un dé. Cela n'aurait donc aucun sens d'utiliser une courbe continue pour représenter la distribution. Il faut cependant bien comprendre que rien n'empêche d'avoir une distribution rectangulaire théorique représentable sur un axe des X à valeurs continues. Par exemple, si on demande à un ordinateur de tirer des milliards de valeurs au hasard entre 0 et 1, de telle façon que chaque point ait la même probabilité de sortir que les autres, on obtiendra une distribution rectangulaire, mais dont les valeurs se répartissent sur un axe à valeurs continues.