Statistique descriptive

Parfois, la relation que nous imaginons entre deux variables n'est pas simplement l'existence d'une co-occurrence, mais traduit véritablement une causalité, c'est-à-dire que la variable A est une cause de la variable B . Par exemple,l'observation que plus les enfants sont âgés et plus leurs capacités intellectuelles augmentent, traduit une relation de cause à effet :c'est parce qu'il y a maturation biologique (avancée en âge de l'enfant) que les performances intellectuelles s'améliorent (par exemple du fait de la myélinisation des neurones).

Il est clair que pour le chercheur comme pour le diagnosticien, obtenir des relations véritablement causales est beaucoup plus intéressant que de constater de simples co-occurrences. En effet, une relation causale donne une perspective d'action, de prédiction. Si je sais que la cause d'une maladie est une bactérie, je peux aussitôt agir sur cette maladie en mobilisant mes connaissances sur ce qui lutte contre les bactéries. À l'inverse, si je sais que c'est un virus, je peux éviter de polluer l'environnement avec des antibiotiques qui seront de toute façon inefficaces. Cette plus grande efficience explique que l'étude logique de la causalité est un sujet qui remplit des manuels entiers de philosophes et de mathématiciens. Les psychologues, cognitivistes ou sociaux, travaillent aussi activement sur la perception de la causalité chez l'humain aussi. Nous n'avons pas l'ambition de passer ces travaux en revue ici. Tout ce qui nous intéresse est de vous donner quelques notions de base qui permettent de comprendre les problèmes posés par l'identification de la causalité à partir de données empiriques.

Afin de faire comprendre le problème qui se pose à nous, commençons par examiner différents types de relations causales. Nous partons du constat d'une co-occurrence régulière entre certaines valeurs d'une variable A et certaines valeurs d'une variable B. Comment peut-on les interpréter ?

3.1. Quelques interprétations au moyen de dépendances causales

Pour ces exemples, prenons l'observation de co-occurrence entre les valeurs d'une variable A (grossir) et une variable B (être fatigué). On observe que les gens qui grossissent tendent à être fatigués et réciproquement que les gens fatigués tendent à grossir. Comment interpréter cela ? Évidemment, une première interprétation consiste à se dire que la co-occurrence est purement fortuite : c'est par hasard qu'elle s'est manifestée dans nos données et si l'on recommence les mesures, il est probable que cette observation ne se réplique pas. Éliminer cette interprétation est un point très important qui fait l'objet des statistiques inférentielles et à ce titre ne ressort pas du présent cours. Aussi, dans la suite, supposerons-nous que la relation existe vraiment. La question est de l'interpréter.

La première forme de la relation causale est l'implication A → B. Les gens seraient fatigués parce qu'ils grossissent.

La deuxième forme de la relation causale est l'implication B→A. Cette fois, c'est la fatigue qui ferait grossir.

La troisième forme passe par l'intervention d'une troisième variable, C, qui cause à la fois A et B, d'où la cooccurrence observée. Par exemple, le facteur stress sera la cause commune : le stress engendre le sentiment de fatigue et d'un autre côté une hormone de résistance au stress aurait pour effet de stocker les graisses, d'où grossissement.

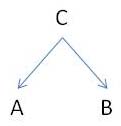
Une quatrième forme consiste à ce que la relation causale entre A et B soit réalisée par l'intermédiaire de la variable C : A → C → B. Par exemple, si on grossit ( A ), on tend à ronfler plus ( C ), ce qui secondairement dégrade la qualité du sommeil, d'où fatigue ( B ). Du coup, si quelque raison s'oppose à la réalisation de C suite à A, la réalisation de B ne surviendra pas non plus. Par exemple, si Marie veut lire tard à la bibliothèque ( A ), elle lira tard à la bibliothèque ( B )... sauf si la bibliothèque n'est pas ouverte (non C ) !

Enfin, une dernière forme de relation peut expliquer pourquoi, parfois, on observera B sans observer A

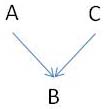
En effet, si A est absent, mais que C aussi peut être la cause de B, alors il suffit que C soit présent pour que B soit présent malgré l'absence de A.

On voit donc qu'il y a très loin du constat d'une co-occurrence à l'adoption d'une relation causale qui explique la co-occurrence de façon certaine.

3.2. La causalité permet la prédiction

Laissons maintenant de côté la question épineuse de l'identification du type de relation qui relie les variables A et B pour nous intéresser à une conséquence importante de la causalité : la capacité de prédire.

Intuitivement, si A et B sont en relation causale, disons que A est la cause de B, alors des variations sur A doivent s'accompagner de la présence de variations concomitantes sur B. Il existe une technique qui permet d'évaluer cette capacité de prédiction : la technique dite de régression, que nous examinerons dans l'article suivant.