Échelles de mesure (Tout est-il mesurable ? )

L'échelonnement des objets d'un ensemble E sur une échelle ordinale repose sur l'établissement d'une relation d'ordre, généralement réflexive, sur les objets (ou éléments) de cet ensemble. Autrement dit, pour tout couple 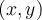$(x, y)$ d'éléments de E, il faut pouvoir décider si la proposition "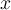$x$ est inférieur ou égal à 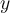$y$"est vraie ou fausse.

Il est courant en Psychométrie d'ordonner les items d'un test selon ce que l'on appelle leur niveau de difficulté. Si tout item est caractérisé par son propre niveau de difficulté, il est le seul représentant de sa classe d'équivalence.

Le niveau de difficulté d'un item est défini relativement à une population de n répondants. Considérons que la réponse aux items est cotée 0 pour "incorrect" et 1 pour "correct". On peut affecter à chaque item le nombre de répondants ayant produit une réponse correcte. On peut ensuite comparer ces nombres à l'aide de la relation "est inférieur ou égal à", ce qui permet d'ordonner les items selon un critère "empirique" et, dirons-nous, de manière plus contemporaine, selon un critère opératoire bien défini. Il serait cependant naïf, et erroné, de considérer que la "difficulté" d'un item est une caractéristique inhérente à l'item, si on fait passer le test à une autre population de répondants, rien ne prouve que le niveau de difficulté des items demeurera identique à ce qu'il était relativement à une première population de répondants. Considérer qu'un item possède la propriété d'être plus ou moins difficile indépendamment d'une population de répondants est une forme de réification.

Un autre exemple d'échelle ordinale est fourni par les scores psychométriques composites. Cet exemple mérite qu'on y consacre une attention particulière, car il est implicitement admis, à tort, que les scores composites constituent un ordre total. Considérons un test composé de k items cotés 0 ou 1. On peut définir une relation d'ordre total sur les réponses de chaque item du test. En revanche, lorsqu'on considère l'ensemble des k-uplets de réponses au test, on ne peut définir qu'un ordre partiel.

Prenons un exemple concret pour illustrer ce point subtil.

Soit la réponse (0, 0, 1, 1) pour un test composé de quatre items ; soit pour le même test la réponse (0, 0, 0, 1) : dans ce cas, on a (0, 0, 0, 1) est inférieur ou égal à (0, 0, 1, 1), puisque :

• 0 est inférieur ou égal à 0,
• 0 est inférieur ou égal à 0,
• 0 est inférieur ou égal à 1,
• 1 est inférieur ou égal à 1.

Considérons maintenant les réponses (0, 0, 1, 1) et (1, 1, 0, 0). On a :

• 0 est inférieur ou égal à 1,
• 0 est inférieur ou égal à 1,
• 1 n'est pas inférieur ou égal à 0,
• 1 n'est pas inférieur ou égal à 0.

Les deux réponses ne sont pas comparables : (0, 0, 1, 1) n'est pas inférieur ou égal à (1, 1, 0, 0) d'une part et (1, 1, 0, 0) n'est pas inférieur ou égal à (0, 0, 1, 1) d'autre part. La relation "est inférieur ou égal à" est donc un ordre partiel sur l'ensemble de k-uplets de réponses, puisqu'il existe au moins deux éléments qui ne sont pas comparables.

En pratique, un ordre total est obtenu en remplaçant les réponses par la somme des codes qui caractérisent les réponses élémentaires. Il faut néanmoins remarquer que l'opération "+" sur des codes ordinaux n'est pas définie. C'est pourquoi les scores composites définissent un ordre total par convention. Cette convention repose sur le fait que les réponses dont les codes ont la même somme sont considérées comme appartenant à une classe d'équivalence, elle aussi conventionnelle. Le fait de considérer que les réponses que l'on regroupe dans une classe d'équivalence sont équivalentes peut être considéré comme une "approximation nominale".

Le programme de psychométrie de L3 présentera des modèles sophistiqués qui ont pour but de surmonter cette difficulté logique grâce à l'hypothèse que les items mesurent de manière probabiliste une unique grandeur psychologique. Le programme de psychométrie de L2 présentera des modèles plus faciles d'accès basés sur la même hypothèse.