Psychométrie : théorie et applications
Le titre développé de cette grande leçon est « Du qualitatif au quantitatif : théorie et applications ». Consacrée à la psychométrie, elle approfondit la problématique de la mesure en psychologie selon deux perspectives.
- D’une part, il s’agit d’expliciter la construction d’un observable comme le processus de composition d’applications, processus qui permet de transcrire des énoncés qualitatifs en énoncés quantitatifs.
- D’autre part, il s’agit de montrer comment l’utilisation des prévisions qu’il est possible de dériver statistiquement à partir des « sorties » de l’observation psychotechnique étaye l’intervention du psychologue dans des problématiques de dépistage, de sélection et de conseil.
1. Ordre simple
1.3. Exercice corrigé
On considère un test composé de deux items cotés dans {0, 1}. Définir l'échelle des scores S en considérant que le score compte le nombre de réponses correctes (cotées 1). Montrer que la relation ≤ définie sur S est un ordre simple. (Cette démonstration est très formelle, mais elle doit être acquise dans son principe pour aller plus loin avec des objets non numériques, comme, en particulier, des phénomènes observés en psychologie).
L'espace d'échantillonnage du test est E = {00, 01, 10, 11}. On obtient donc l'échelle S = {0, 1, 2}. La relation ≤ définie sur S est un ordre simple si elle est transitive, antisymétrique, et fortement complète.
Transitivité : on considère les 3×3×3 triplets de nombres possibles et on vérifie que 
et 
, c'est-à-dire que si on a et 
, alors on a aussi 
. Les vérifications sont listées ci-dessous.
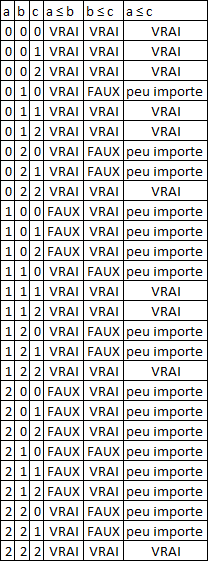
Antisymétrie : on considère les 3×3 couples de nombres possibles et on vérifie que et 
. Les vérifications sont listées ci-dessous.
Complétude forte : on considère les 3×3 couples de nombres possibles et on vérifie que ou 
. Les vérifications sont listées ci-dessous.
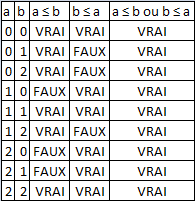
La relation ≤ définie sur S est transitive, antisymétrique et fortement complète, donc c'est par définition une relation d'ordre simple.