Statistique : comparer des moyennes
Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
5. Comparaisons planifiées dans l'ANOVA : contrastes
5.3. Le test statistique du contraste
On peut passer soit par un test du F soit par un test du t de Student mais dans les deux cas la formule utilisée passe par le calcul du carré moyen du contraste.
3.1. Remarque préliminaire importante
Les tests qui suivent sont déterminés pour un contraste particulier. Lorsque plusieurs hypothèses cibles permettent de planifier plusieurs contrastes, il faut limiter l'erreur de l'ensemble des comparaisons cibles (voir l'article sur les comparaisons multiples et plus particulièrement la page sur la correction de Bonferroni). Ce qui, nous l'avons vu, suppose de se donner un critère plus sévère pour chaque comparaison.
Rappelons que si l'on se donne α comme critère acceptable pour la significativité de l'ensemble EC des k comparaisons cibles (ici les contrastes), on se donnera comme critère pour chaque contraste élémentaire :
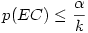
3.1. Calcul du carré moyen du contraste
Un contraste n'a qu'un seul degré de liberté puisque c'est une comparaison entre deux agrégats (et donc 2-1=1 ddl), Et puisque le carré moyen est la somme des carrés divisée par le nombre de degrés de liberté, le CM d'un contraste est en réalité égal à sa somme des carrés. C'est cette dernière qu'il nous faut calculer.
Cette somme ne dépend que des moyennes des groupes à agréger, des coefficients choisis, et des effectifs.
Nous avions vu que le contraste Ψ est facile à calculer comme une simple somme pondérée à partir des moyennes des groupes pris en compte et des coefficients choisis
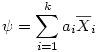
L'on a alors dans le cas général :
qui dans le cas d'effectifs équilibrés (tous les n1 = n2 = ... = n ) se simplifie en
3.2. Test statistique du contraste
3.2.1. par le
F
de Fisher
Le test est facile à réaliser à la main. Il s'agit de traiter le contraste comme un facteur à deux groupes dans une ANOVA, calculer le F de Fisher et la valeur p associée selon la méthode habituelle, à savoir
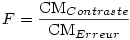
Si les deux agrégats comprennent n sujets, les degrés de liberté seront donc 1, puisqu'il y a deux agrégats, et n -1 pour les degrés de liberté de l'erreur.
Le calcul du carré moyen de l'erreur est simplissime puisque c'est tout simplement le même que celui de l'ANOVA globale ! Donc nous ne reviendrons pas dessus.
3.2.1. par le t de Student
On trouve aussi dans les logiciels de statistique un test par le t de student. Mais ici la valeur de t peut s'obtenir en prenant la racine carré du F puisque dans le cas particulier où il n'y a que deux groupes (ou deux agrégats dans le cas d'un contraste), F = t ²
Voyons maintenant la notion de contrastes orthogonaux.