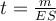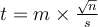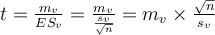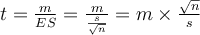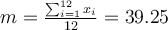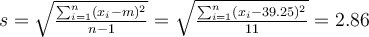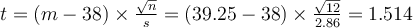Statistique : comparer des moyennes
 Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
2. Comparer deux moyennes : test du t de Student
2.2. Comparer un échantillon contre une constante

- 1. Il faut soit avoir un échantillon de données recueillies à raison d'une seule valeur par sujet, soit deux échantillons d'un même type de mesures (par exemple, un temps de réponse dans les deux cas) recueillis à raison de deux données par sujet et sur lesquelles on peut procéder à une différence, laquelle sera comparée à une constante, généralement 0, mais pas nécessairement.
- 2. Les données de l'échantillon devraient idéalement être normalement distribuées. Cliquez ici pour accéder à l'article expliquant comment vérifier si cette condition est réalisée.
- 3. Il faut disposer d'une hypothèse sur une valeur de référence. Par exemple, si l'on connaît la valeur moyenne de la variable mesurée dans la population de référence, comparer l'échantillon à cette valeur de référence permet de tester s'il est raisonnable de considérer que notre échantillon provient bien de la population de référence.
- 4. L'hypothèse nulle est ici la suivante : m = c. Ou encore, ce qui revient au même m - c = 0. Par exemple, si l'on veut tester une hypothèse selon laquelle l'intelligence générale augmente de génération en génération depuis qu'on la mesure (ce qu'on appelle "l'Effet Flynn"). Supposons qu'on dispose d'un test utilisé il y a trente ans. On sait qu'à l'époque une performance donnée sur le test correspondait à l'époque à la valeur de QI=100. On fait passer le test à des jeunes actuels. On observe donc une nouvelle moyenne. On va alors comparer cette moyenne à la valeur de référence 100. Et si l'on trouve que le QI actuel est significativement supérieur à 100 tel que mesuré sur cet outil utilisé à l'époque, alors on pourra conclure que le QI a monté.
Voir aussi : vidéo de savoir-faire sur le test de student à échantillon unique par logiciels
Préalables spécifiques de cette version du test de Student :
2.1. Obtenir la valeur de
t
2.1.1. Pour les pressés : "En très bref"
Soit notre échantillon réel de taille n, de moyenne m et d'écart-type s, et soit c la constante à laquelle on veut le comparer.
Selon les informations dont on dispose, on applique la formule avec l'erreur standard ES,
ou, ce qui revient au même, celle avec l'effectif et l'écart-type d'échantillon,
On présente le résultat en écrivant t(ddl)=n.nn (pour la présentation de la valeur p, voir l'article général sur la norme APA de présentation du t).
Voir aussi le lien de pratique avec les logiciels de statistiques :
_
Interpréter des résultats de test t à échantillon unique
2.1.2. Pour ceux qui aiment comprendre : D'où cela vient-il ?
Dans le test du t de Student, la statistique calculée est précisément la valeur t. Dans le cas de la comparaison d'un échantillon contre une constante, voyons quelle formule employer. Commençons par rappeler la formule générale du t :
Soient mv la moyenne d'un échantillon virtuel de taille nv et ES v son erreur-standard, on a
Ici notre échantillon virtuel a pour moyenne
mv
=
(m
-
c)
où m
est la moyenne de l'échantillon réel et
c
la constante à comparer. Et on a aussi
ESv
=
ES, où ES est l'erreur standard de l'échantillon réel.
Démonstration. Ce dernier point résulte des propriétés générales de la variance : si l'on construit une nouvelle variable en faisant pour chaque sujet la différence entre la variable de départ et une constante, la variance de la variable d'arrivée est la même que la variance de la variable de départ. Ce qui se comprend aisément puisque la variance étant la dispersion de la variable, la nouvelle variable est tout aussi dispersée que la première ! Les échantillons virtuels et réels ont aussi, dans ce cas, la même taille. Puisque la formule de l'erreur-standard ne dépend que de la variance et de l'effectif, les deux erreurs-standard sont donc égales. CQFD.
Application : De ce qui précède, il suit que
2.2. Comment obtenir la valeur p associée ?
Il nous faut connaître la valeur t bien sûr et le nombre de degrés de libertés.
Ici l'échantillon virtuel a la même taille que l'échantillon réel, soit n individus. Le nombre de degrés de libertés est directement ddl=n -1.
Si elle n'est pas directement donnée par votre logiciel de statistique, la valeur p associée s'obtient
- soit en regardant dans une table du t de student en prenant comme entrée la valeur du t ainsi calculée et comme nombre de degrés de libertés la valeur n -1 où n est le nombre de mesures.
-
Soit au moyen d'une formule de tableur sous Microsoft Office Excel ou OpenOffice Calc : "=LOI.STUDENT.BILATERALE(
t
;
ddl
)"
2.3. Unilatéral ou bilatéral ?
Par défaut, on travaillera en bilatéral et on se contentera de la valeur p précédemment obtenue.
Si toutefois on dispose d'une hypothèse orientée et que les statistiques descriptives vont dans le sens attendu (typiquement, on s'attend à ce que m > c et c'est le cas au niveau descriptif, ou bien, on s'attend à ce que m < c et c'est le cas au niveau descriptif), alors on peut travailler en unilatéral : Il suffit alors de prendre la valeur p précédemment obtenue et la diviser par deux avant de décider si le test est significatif ou non.
2.4. Un exemple
Supposons que l'on ait une hypothèse théorique selon laquelle les astronautes en général (qu'ils aient ou non marché sur la lune) devraient avoir plus de 38 ans en moyenne.
Imaginons que la seule information dont nous disposions est l'âge des astronautes qui ont marché sur la lune au moment de leur sortie sur notre satellite. Nous obtenons le tableau suivant :
| Individu | Age |
| 1 | 38 |
| 2 | 39 |
| 3 | 39 |
| 4 | 37 |
| 5 | 47 |
| 6 | 39 |
| 7 | 39 |
| 8 | 41 |
| 9 | 41 |
| 10 | 36 |
| 11 | 38 |
| 12 | 37 |
À partir de ce tableau, il est facile de calculer la moyenne et l'écart-type des âges, soit
et
Attention au fait que dans ce cas, le tableau représente un échantillon de la population cible totale (les astronautes en général) et l'on utilise la formule de l'écart-type pour échantillon (on divise par n -1) et non de l'écart-type pour population (où l'on divise par n).
Nous obtenons
Ensuite, sous excel par exemple, en appliquant la formule =LOI.STUDENT.BILATERALE(t
;
ddl)" avec le
t
que l'on vient de calculer et
ddl
=12-1=11 degrés de libertés, on trouve
p
=0.15820928.
Pour un test du t, la question suivante à se poser concerne le caractère bilatéral ou non du test. Ici, on a une hypothèse précisant que la moyenne attendue doit être supérieure à 38. C'est bien le cas puisque la moyenne observée est 39.25. Nous sommes donc fondés à travailler en unilatéral et nous divisons simplement la valeur p précédente par 2, ce qui donne 0.08508. Finalement, on peut rapporter le résultat inférentiel, conformément aux normes :
t (11)=1.51, p =.079 en unilatéral, ce qui n'est pas significatif, mais indique néanmoins une tendance.