Statistique : comparer des moyennes
Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
2. Comparer deux moyennes : test du t de Student
2.4. Comparer deux échantillons appariés.
L'hypothèse nulle est ici la suivante :
m
1
=m
2
. Ou encore, ce qui revient au même,
m
1
-m
2
=0. Par exemple, si l'on a fait une comparaison avant-après, en faisant la différence des deux valeurs obtenues pour chaque sujet, on obtient une nouvelle variable qu'il suffit de comparer, par un test à un échantillon vu précédemment, contre la valeur de référence 0. On pourra ensuite interpréter la différence en termes de progression : si la moyenne est significativement supérieure à 0 il y aura eu augmentation, si la moyenne est significativement inférieure à 0 il y aura eu diminution. Enfin, si la différence n'est ni significativement supérieure ni significativement inférieure à zéro, on ne peut pas dire qu'il y a un effet avant-après.
Préalables spécifiques de cette version du test de Student :
1. Il faut avoir deux échantillons d'un même type de mesure (par exemple, un temps de réponse dans les deux cas) recueillis à raison de deux données par individu statistique et sur lesquelles on peut procéder à une différence.
2. Les données de l'échantillon devraient idéalement être normalement distribuées. Cliquez ici pour accéder à l'article expliquant comment vérifier si cette condition est réalisée.
2.1. Obtenir la valeur de
t
2.1.1. Pour les pressés : "En très bref"
À partir des deux échantillons de données appariées, on construit la variable de différence en calculant pour chaque ligne i , la valeur xi = x i1 - xi 2 . Cela nous donne un échantillon réel de taille n (ici n couples de données), de moyenne m et d'écart-type s.
Selon les informations dont on dispose, on applique la formule avec l'erreur standard ES,
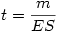
ou, ce qui revient au même, celle avec l'effectif et l'écart-type d'échantillon,
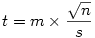
On présente le résultat en écrivant t ( ddl )=n.nn (pour la présentation de la valeur p , voir l'article général sur la norme APA de présentation ).
2.2. Comment obtenir la valeur p associée ?
Il nous faut connaître la valeur t bien sûr et le nombre de degrés de liberté.
Ici l'échantillon virtuel a la même taille que l'échantillon réel, soit n individus. Le nombre de degrés de liberté est directement ddl=n -1.
Si elle n'est pas directement donnée par votre logiciel de statistique, la valeur p associée s'obtient
- soit en regardant dans une table du t de student en prenant comme entrée la valeur du t ainsi calculée et comme nombre de degrés de liberté la valeur n -1 où n est le nombre de mesures.
-
Soit au moyen d'une formule de tableur sous Microsoft Office Excel ou OpenOffice Calc : "=LOI.STUDENT.BILATERALE(
t
;
ddl
)"
2.3. Unilatéral ou bilatéral ?
Par défaut, on travaillera en bilatéral et on se contentera de la valeur p précédemment obtenue.
Si toutefois on dispose d'une hypothèse orientée et que les statistiques descriptives vont dans le sens attendu (typiquement, on s'attend à ce que m > 0 et c'est le cas au niveau descriptif, ou bien on s'attend à ce que m < 0 et c'est le cas au niveau descriptif), alors on peut travailler en unilatéral : il suffit alors de prendre la valeur p préalablement obtenue et la diviser par 2 avant de décider si le test est significatif ou non.
2.4. Un exemple
Dans une expérience sur le risque lié à l'alcool, on a demandé à chacun des 31 participants d'évaluer le risque associé à une situation de conduite sur une échelle de 1 à 5.
On a obtenu, en rangeant les données à raison d'une ligne par sujet, le tableau suivant :
| Sansalcool | Avec alcool | Différence |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 4 | 3 |
| 1 | 4 | 3 |
| 1 | 4 | 3 |
| 1 | 4 | 3 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 4 | 3 |
| 1 | 5 | 4 |
| 1 | 4 | 3 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 2 | 5 | 3 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 4 | 3 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 2 | 4 | 2 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 3 | 2 |
| 2 | 5 | 3 |
| 1 | 5 | 4 |
| 1 | 3 | 2 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 3 | 2 |
| 1 | 4 | 3 |
En première approximation, on a constaté que la moyenne de la situation sans alcool est de 1.10 alors que la colonne 2 est en moyenne à 4.52. Descriptivement, on pourrait donc dire que les participants jugent la situation 2 plus risquée que la situation 1... mais est-ce vrai statistiquement ?
La troisième colonne a été obtenue en faisant la différence de la colonne 2 (avec alcool) et de la colonne 1 (sans alcool). Nous allons travailler à partir de cette colonne.
À partir de ce tableau, il est facile de calculer la moyenne et l'écart-type des différences, soit
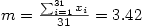
Pour ceux qui se rappellent que la moyenne des différences est égale à la différence des moyennes (les effectifs étant ici égaux), cette moyenne est sans surprise puisque 5.52 - 1.10 = 3.42.
Pour l'écart-type,
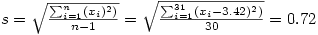
Nous obtenons
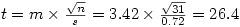
Ensuite sous Excel par exemple, en appliquant la formule =LOI.STUDENT.BILATERALE( t ; ddl )" avec le t que l'on vient de calculer et ddl=31-1=30 degrés de libertés, on trouve p =2.4x10 -22, ce qui est quasiment égal à zéro. Autrement dit, ce n'est même pas la peine de se poser la question de la latéralité : de toute façon le test est très nettement significatif.
Finalement on peut rapporter le résultat, conformément aux normes :
t (30)=26.4, p< .001, ce qui est significatif : on peut donc conclure que la situation 2 est jugée plus risquée par les participants que la situation 1.