Statistique : comparer des moyennes
Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
3. Comparer plus de deux moyennes : L'ANOVA à un facteur
3.4. Somme des carrés et carré moyen
A. Relations entre Somme des carrés, Variance et Carré moyen
On appelle Somme des carrés (SC en abrégé en français, ou encore SS pour "Sum of Squares" en anglais), le numérateur de la formule générale de la variance. La formule générale de la variance peut donc se ré-écrire :
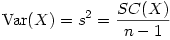
Nous avons vu dans le cours sur le t de Student que le nombre de degrés de liberté de la moyenne d'un groupe de mesures est égal au nombre de sujets - 1
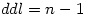
Du coup, on peut réécrire ainsi la formule précédente
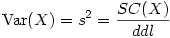
On appellera alors cette expression le carré moyen de l'échantillon, que l'on abrégera par CM en français et MS pour Mean Square en anglais.
Le carré moyen n'est donc qu'un autre nom pour la variance d'échantillon et c'est ce carré moyen qui est généralement présenté dans les tableaux d'analyse de variance fournis par les logiciels de statistique.
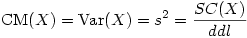
Attention : dans certains tableaux, il existe des formules de la variance d'échantillon et des formules de la variance de population. Si vous calculez vos sommes de carrés à partir de ces formules (puisqu'il suffit de multiplier le carré moyen, donc la variance, par le nombre de degrés de libertés pour avoir la somme des carrés) ne vous trompez pas et utilisez la variance d'échantillon, car dans la variance de population la somme des carrés n'est pas divisée par le nombre de degrés de libertés ( N -1) mais par l'effectif complet (N).
B. Des "Types" de sommes de carrés ??
Dans les logiciels de statistique, vous trouverez mentionnée l'existence de sommes des carrés "de type III" ou "de type VI". Il s'agit là de raffinements de la notion de calcul des sommes de carrés dans les ANOVA à plusieurs facteurs lorsque les plans sont déséquilibrés (les effectifs entre les groupes sont inégaux). Ce n'est pas du niveau du présent cours et nous nous bornerons ici à en signaler l'existence.