Statistique : comparer des moyennes
Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
3. Comparer plus de deux moyennes : L'ANOVA à un facteur
3.9. ANOVA et calcul des valeurs-p
8.1. Calcul de la valeur
F
Si l'on calcule le rapport entre la variance intra-groupe et la variance totale, la statistique obtenue, que l’on appelle F , suit une loi dite de Loi de Fisher-Snedecor.
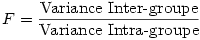
Et puisque dans l'ANOVA la variance est donnée par le carré moyen, pour obtenir le F nous n'avons qu'à faire la division du CM Inter par le CM Intra . L'exemple numérique précédent est clair dans le tableau de résumé de l'ANOVA :
F = 48.552 / 16.833 = 2.88428
8.2. Obtention du
p
à partir du
F
8.2.1. Principe
La loi normale utilise deux paramètres : la moyenne et la variance. La loi normale centrée-réduite n'en a plus aucun, car il s'agit de la loi normale pour lesquelles la moyenne a été fixée à 0 et l'écart-type à 1. La loi de Student représente une sorte de famille de variantes de la loi normale centrée réduite, où chacune des variantes est déterminée par la valeur d’un paramètre particulier, le nombre de degrés de liberté. Ainsi pour chaque degré de liberté, on peut calculer une loi de Student particulière. Dans le cas de la loi du F , les choses gagnent un cran de complexité puisque la loi du F est une famille de variantes dont chacune est déterminée, non par un seul mais par deux degrés de liberté. Spécifiquement, il s’agit (1) du nombre de degrés de liberté du facteur, qui est tout simplement donné par le nombre de groupes – 1 ;et (2) le nombre de degrés de liberté intra-groupes, ou "nombre de degrés de liberté de l’erreur", qui est le nombre de sujets moins le nombre de groupes.
Partant de là, en appliquant les mêmes principes que nous avons déjà vus à propos de la loi normale, ou de la loi de Student, on peut mettre en relation une valeur donnée de F, celle observée dans les données, avec la probabilité a priori de rencontrer une telle valeur, probabilité qui nous est donnée par la loi.
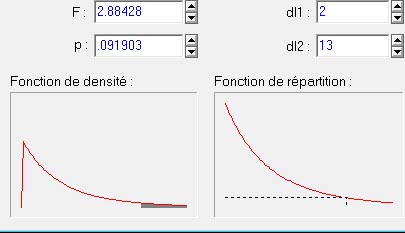
Si nous prenons la valeur du F de l'exemple numérique précédent, voici ce que nous obtenons (image générée à partir du logiciel Statistica) :
Le graphique en bas à gauche de la figure ci-dessus représente la courbe de la distribution théorique du F de Fisher pour une variance inter à 2 degrés de liberté et pour 13 degrés de liberté intra. La petite région grisée sous la courbe représente la surface relative occupée par les valeurs de F qui sont supérieures ou égales à la valeur indiquée (2.88428). On voit que plus ce F est grand, et plus la surface grisée représentera une proportion faible de la courbe. Ici cela représente 9,903% de la surface totale de la courbe : la probabilité d'obtenir par hasard une valeur de F supérieure ou égale à celle que nous avons calculée à partir de nos données n'est que .091903 (valeur p indiquée en haut dans la figure). Dans ce cas, cette valeur n'est pas significative au seuil de 5% puisque le risque pris en rejetant l'hypothèse dépasse 5%, ce qui n'est pas acceptable dans les conventions classiques.
Il existe des tables de cette loi, mais de nos jours les logiciels de statistique et même les logiciels tableurs (eg., Microsoft Excel, ou OpenOffice Calc) donnent directement la valeur p . Par exemple, sous Excel, la fonction "=LOI.F(F;ddl1;ddl2)" où l'on remplace F, ddl1, et ddl2 par les paramètres que nous avons calculés précédemment, cette fonction donc retourne directement la valeur 0.091903.
8.2.2. Mise en garde concernant les tests unilatéraux
Une différence majeure existe entre d’un côté la loi normale et la loi de Student, et de l'autre côté la loi du F. Si nous regardons la forme de la loi du F (figure plus haut), nous voyons que cette loi n’est pas symétrique, contrairement aux deux précédentes. Cette caractéristique a une importance majeure d’un point de vue calculatoire : on ne peut pas appliquer la technique des tests unilatéraux avec des statistiques F comme on le faisait avec les tests t. Rappelons que le test unilatéral repose sur l’idée que l’hypothèse étant orientée, si les résultats observés vont dans le sens attendu, on peut diviser par deux la valeur p obtenue puisque seule la moitié de l’aire sous la courbe de la loi est pertinente. Cette possibilité n’a aucun sens pour la loi du F.