UOH / Statistique et Psychométrie en L1

A. La médiane

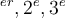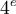Considérons une variable ordinale. Il s'agit, rappelons-le, une variable dont les modalités (ou les valeurs, lorsqu'il s'agit d'une variable continue) sont ordonnées les unes par rapport aux autres. C'est le cas par exemple des rangs d'arrivée dans une course (1$^{er}, 2^e, 3^e$ et $4^e$ ex-aequo, etc.). Il est clair que cela n'a aucun sens d'additionner ces nombres : ici 1+2 n'est pas égal à 3. 1+2 ne veut simplement rien dire. Comme la moyenne est avant tout une somme pondérée par le nombre d'observations, il n'a donc aucun sens de calculer une moyenne avec de tels nombres. Nous devons donc nous donner un autre indicateur de centralité que la moyenne.

L'indicateur de centralité privilégié pour les données ordinales est la médiane.

En effet, puisqu'une relation d'ordre traduit une disposition des observations entre elles, l'indice de centralité traduit le centre d'un classement : c'est le point tel que la moitié des observations sont plus grandes et l'autre moitié des observations sont plus petites. En fait, le détail du calcul est un peu plus compliqué que cela, car il faut tenir compte du nombre d'observations dans la série, et aussi de la possibilité de l'existence d'ex aequo.

Contrairement à la moyenne qui se définit par une formule, la médiane se définit difficilement par une formule, car son calcul suppose de procéder préalablement à un rangement des données : il faut commencer par ordonner les observations de la plus petite valeur à la plus grande (ou l'inverse). Si nous sommes dans le cas simple où le nombre d'observations est impair et où il n'y a pas d'ex aequo, la médiane est tout simplement la valeur de l'observation du milieu, puisque la moitié moins 1 des observations seront plus grandes et la moitié moins 1 des observations seront plus petites.

On l'aura compris, le premier avantage de la médiane est de ne pas nécessiter plus de propriétés qu'une simple relation d'ordre entre les nombres. Du coup, on peut l'utiliser même si la somme n'a aucun sens.

Le deuxième avantage est que la médiane n'est pas sensible aux valeurs extrêmes.

Par exemple, prenons la série de trois observations suivantes : 2; 5; 20.

La moyenne est 27 / 3 = 9. La médiane est 5.

Imaginons que, suite à un problème, la troisième valeur soit 500. La moyenne devient 169 tandis que la médiane reste à 5. On voit donc que la médiane n'est tout simplement pas sensible au niveau d'éloignement des valeurs, seulement à leur rang.

L'inconvénient évidemment, c'est que si l'éloignement extrême de la valeur était justifié, cette absence de prise en compte constitue une perte de sensibilité par rapport à la moyenne.

L'étudiant qui le souhaite pourra trouver sur ce site des tutoriels pour calculer des médianes en cochant simplement la case appropriée dans un logiciel de statistiques (ici jamovi ou R). Le calcul de la médiane par tableur se réalise exactement comme pour calculer des moyennes, mais en utilisant la fonction MEDIANE au lieu de MOYENNE.

B. Le mode

Lorsque la variable étudiée ne possède même pas les propriétés d'une variable ordinale, c'est-à-dire lorsque ses modalités doivent simplement être considérées comme des catégories mutuellement exclusives sans qu'une relation d'ordre les relie, une seule opération est possible : compter simplement combien d'observations se trouvent dans chacune des modalités de la variable.

Dans ce cas, la tendance centrale revient simplement à la modalité qui possède le plus d'observations : c'est ce qu'on appelle le « mode de la variable ». La procédure de calcul d'un mode : on compte le nombre d'observations par modalités de la variable est le mode est la valeur de la modalité la plus fréquente.

Clairement, cet indice est assez pauvre, mais c'est le seul disponible lorsque la variable est nominale. Par contre, si vous rapportez un mode, en tant que valeur de la modalité dominante, pensez à rapporter en même temps le pourcentage d'observations qui se sont concentrées sur le mode. Ainsi, on obtient une information supplémentaire sur le degré de dominance de ce mode.

Dire que le mode peut être plus ou moins dominant, c'est remarquer que les données sont plus ou moins dispersées dans les différentes modalités. Cela nous mène à l'article suivant, qui concerne les indices permettant d'évaluer la dispersion des données.