Statistique descriptive
 Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Rédaction : Éric Raufaste
3. Indices de dispersion
3.1. Dispersion des variables numériques
A. Min, Max et Étendue
L'étendue, ou intervalle de variation, est la plus simple des mesures de dispersion que l'on peut obtenir avec des variables numériques. Il s'agit tout simplement de la différence entre la valeur la plus forte et la valeur la plus faible. Si l'on a une variable numérique X, et que l'on note Max(X) la valeur la plus forte et Min(X) la valeur la plus faible, on a donc :
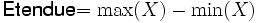
Pour information, le min et le max d'une série de données sont directement accessibles comme des fonctions de tableur, au même titre que la somme ou la moyenne.
Dans le cas de variables numériques, l'interprétation naturelle de l'étendue est une distance : la distance maximale qui sépare deux données de l'échantillon.
Lorsque l'on travaille avec des données empiriques, éventuellement issues d'un recodage, il est important de regarder les valeurs Min et Max, car c'est un moyen simple de détecter des erreurs de saisie. Si vous avez une échelle de mesure qui permet d'avoir des notes de 0 à 10 par exemple, et que le max dépasse 10, c'est nécessairement qu'une erreur de saisie a été commise. Ce type d'erreur est très fréquent, et presque inévitable lorsque les données sont nombreuses et que leur saisie n'est pas réalisée par l'intermédiaire d'un programme informatique capable de les détecter au moment même de la saisie. Or une seule erreur de ce type peut changer très sensiblement les calculs de moyenne ainsi que les calculs des variables de dispersion que nous allons voir maintenant.
Parfois, certaines valeurs sont ainsi très différentes des autres, sans correspondre à des erreurs de saisie ou de logiciel. On parle de valeurs aberrantes (en anglais «outliers»). Par exemple, on enregistre des temps de réponse sur une tâche à laquelle les sujets mettent en général 2 à 3 secondes à répondre. Et on observe que pour certaines observations, le temps dépasse une minute. Il est donc très probable que quelque chose d'anormal s'est passé au moment du recueil pour ces sujets.
B. Variance et écart-type
Variance et écart-type d'une population
La variance représente une dispersion. L'idée de base est que la dispersion s'évalue à partir d'une valeur centrale : plus les observations sont loin de la valeur centrale, et plus elles sont dispersées. Puisqu'on est dans un cas où la variable est numérique, la valeur centrale que l'on pourra prendre sera naturellement la moyenne. Une valeur donnée sera donc d'autant plus dispersée qu'elle sera loin de la moyenne
 . En première approximation, il pourrait donc suffire de calculer la moyenne des écarts à la moyenne pour avoir une évaluation de la dispersion des données de l'échantillon. Pour une raison que nous détaillerons ensuite, on préfère cependant calculer la moyenne des carrés des écarts à la moyenne.
. En première approximation, il pourrait donc suffire de calculer la moyenne des écarts à la moyenne pour avoir une évaluation de la dispersion des données de l'échantillon. Pour une raison que nous détaillerons ensuite, on préfère cependant calculer la moyenne des carrés des écarts à la moyenne.
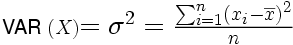
et l'écart-type de la population pourra alors aussi être calculé comme la racine carrée de la variance, soit
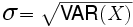
Pourquoi prend-on la somme des carrés des écarts, et pas les écarts eux-mêmes ?
Pour répondre à cette question, imaginons que nous ayons deux mesures, une qui représente la moyenne +1 et l'autre qui représente la moyenne-1. Par exemple, sur la figure ci-dessous, la moyenne est m et la dispersion de ces deux mesures est représentée par l'accolade qui relie m -1 et m +1.
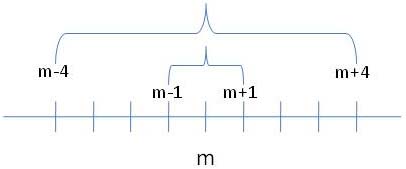
Si je fais la somme des écarts de ces deux données à la moyenne, j'obtiendrai 1-1 = 0. Imaginons maintenant que nous ayons deux autres mesures, une qui représente la moyenne +4 et l'autre qui représente la moyenne -4. Si je fais la somme des écarts à la moyenne de ces deux nouvelles données, j'obtiendrai 4-4 = 0. L'indice obtenu en sommant les écarts à la moyenne n'est donc pas capable de reconnaître que le deuxième couple de données est plus dispersé autour de la moyenne que le premier, chose que l'intuition nous indique pourtant sans effort : il suffit de voir sur le schéma ci-dessus que les deux accolades n'ont pas la même largeur.
L'avantage de sommer les carrés des écarts plutôt que les écarts eux-mêmes tient à ce que les écarts positifs et négatifs ne s'annulent alors plus. ET de ce fait, le carré moyen des écarts du premier couple de données est de 1+1 = 2, divisé par 2, soit 1. Pour le second couple de données, le carré moyen des écarts est 16+16=32... Cette fois, on voit clairement que le second couple est plus dispersé autour de la moyenne que le premier.
Variance d'un échantillon
Bien souvent, en recherche, on ne s'intéresse pas seulement à décrire les caractéristiques d'un échantillon, mais on cherche à se faire une idée des caractéristiques de la population dont l'échantillon est issu. Si on a pris soin de choisir un échantillon bien représentatif de la population cible, celle au sujet de laquelle on veut apprendre quelque chose, alors la moyenne de l'échantillon nous renseigne sur la moyenne de la population, et l'estimation de la taille des écarts nous renseigne sur la dispersion des mesures qu'on aurait dans l'ensemble de la population. On peut montrer qu'une bonne estimation de la variance de la population est obtenue à partir de l'échantillon en divisant la somme des carrés des écarts à la moyenne par n-1 au lieu de n.
Définition. Soit un échantillon de n données mesurées sur une variable X, où Xi représente la ième donnée de la variable X. La variance de cet échantillon est donnée par :
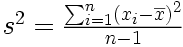
où
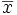 dénote la valeur moyenne de
X.
dénote la valeur moyenne de
X.
Écart-type d'un échantillon
En travaillant avec les carrés, nous avons évité un problème. Toutefois, le résultat obtenu n'est plus dans la même métrique que la valeur qu'on a cherché à mesurer. Par exemple, si on a mesuré des longueurs, la variance traduit bien la dispersion des données de l'échantillon mesures, mais puisqu'on a moyenné des mètres carrés et non des mètres, le résultat n'est pas directement interprétable en termes de la variable cible !
Pour avoir un indice de dispersion qui soit dans la même unité que la variable cible, on est donc conduits à utiliser la racine carrée de la variance et non la variance elle-même : c'est l'écart-type, noté directement s .
C. Variance d'erreur et erreur standard (aussi appelée erreur-type)
Lorsque l'on procède à une expérience, on travaille à partir d'un échantillon et non à partir de la population entière. Si l'on recommence l'expérience avec un autre échantillon, on aura un résultat légèrement différent. Le simple fait de travailler avec un échantillon aléatoire plutôt qu'avec l'ensemble de la population induit une erreur. Une partie de la dispersion totale des mesures est donc due à l'échantillonnage. Si l'on exprime la variabilité par la variance, on dira donc qu'une partie de la variance totale est de la variance d'erreur.
Logiquement, la part de cette variance d'erreur est d'autant plus faible que l'échantillon est grand. Cela a pour conséquence que si l'on veut comparer des dispersions provenant d'échantillons de tailles différentes, ces derniers présenteront des niveaux de biais différents. Par exemple, supposons que l'on compare quatre groupes de sujets. Supposons encore que l'un des groupes soit sensiblement plus petit que les trois autres. En ce cas, la comparaison des dispersions dans ces différents groupes n'est pas possible, sauf à disposer d'une mesure de dispersion moins biaisée par la taille de l'échantillon. Cette mesure, c'est l'erreur standard que l'on obtient en divisant la variance par la racine carrée de l'effectif.
On pourra alors avoir deux cas selon que l'on considère la population ou l'échantillon.
Cas de la population :
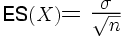
Cas de l'échantillon :
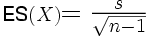
D. Écart absolu moyen (aussi appelé déviation moyenne)
Si vous êtes plus tard amenés à lire certains articles de recherche, vous risquez de rencontrer un autre type de mesure de dispersion que l'on utilise parfois, à savoir la déviation moyenne. La logique est la même que celle de la variance, sauf qu'au lieu d'élever les écarts à la moyenne au carré pour s'affranchir du problème des écarts négatifs qui s'annulent avec les écarts positifs, on ramène tous les écarts à des valeurs absolues avant de les moyenner. Ce qui donne la formule suivante :
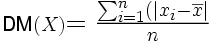
Couleur de fond
Police
Taille de police
Couleur de texte

