UOH / Statistique et Psychométrie en L1

Nous allons retrouver ici la notion d'étendue, vue dans le cas des variables numériques. Toutefois, interpréter une étendue comme une distance n'aurait aucun sens. Lorsque les variables sont ordinales, il ne sert à rien de calculer des sommes et des différences comme on le fait dans les calculs vus précédemment. Par contre, on peut utiliser la relation d'ordre. Autrement dit, on va commencer par ranger les observations de la plus petite à la plus grande (ou l'inverse). On peut alors toujours considérer la dispersion comme une étendue, mais en interprétant cette dernière sous l'angle des valeurs qui permettent de repérer une certaine proportion d'observations.

A. Notion de quantiles

De façon abstraite, si nous avons un échantillon de n observations, nous pouvons le partager en k parties de même effectif. Dans le cas général, on appelle chacun des groupes ainsi obtenus un quantile. Certains quantiles ont des noms particuliers. La médiane est la valeur qui partage l'échantillon en k =2 quantiles, dont le nom est bien connu : ce sont des moitiés.

Par exemple, imaginons que nos observations soient la série des 12 premiers entiers naturels positifs, de 1 à 12. Nos données d'entrées sont donc :

.

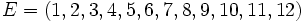La première moitié contient les

.

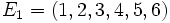et la seconde moitié

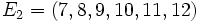
La médiane correspond à une valeur qui partage ces observations en deux moitiés. Nous prendrons donc naturellement 6,5. On voit aisément que tous les éléments de E 1 sont bien inférieurs à 6,5 tandis que tous ceux de E 2 sont supérieurs.

Si k =100, nous appellerons centile des groupes ordonnés d'observations tels que chaque groupe contient 1% des observations. Les percentiles correspondent aux valeurs qui bornent les centiles et non aux intervalles eux-mêmes. Ainsi le 50$^e$ percentile est la médiane.

si k =10, nous appellerons décile, des groupes ordonnés d'observations tels que chaque groupe contient 10% des observations. Le premier décile contient donc les 10% d'observations les plus basses. Le deuxième décile contient 10% d'observations qui sont toutes plus grandes que les valeurs du premier décile (ou égales à la plus grande de ces valeurs en cas d'ex æquo), et qui sont toutes plus petites que les valeurs du troisième décile (ou égales à la plus petite de ces dernières valeurs en cas d'ex æquo).

Munis de cette notion de quantile, nous pouvons exprimer des indices de dispersion ordinaux, qui correspondent alors à des étendues réduites d'un certain nombre des quantiles les plus extrêmes.

B. Quartiles et écarts inter-quartiles

En reprenant la notion de quantile, et si k =4, nous avons 4 quartiles qui correspondent chacun à 1/4 = 25% des observations. Les quantiles qui représentent 1/4 des observations s'appellent des quartiles. Un échantillon possède donc 4 quartiles.

On appelle aussi quartiles, les trois valeurs qui partagent l'échantillon en 4. Dans cette acception, le premier quartile est la valeur Q1 qui partage le premier et le deuxième ensemble de 25% d'observations. Le deuxième quartile, Q2, est la médiane. Le troisième quartile, Q3, est la valeur qui partage le troisième et le quatrième ensembles de 25% d'observations.

On appelle alors Écart interquartile l'étendue comprise entre le troisième et le premier quartile. On peut donc le calculer très simplement en faisant la différence de ces deux valeurs.

Si nous reprenons l'exemple de l'ensemble E d'observations vu plus haut. Le premier quartile contient les 25% d'observations les plus basses soit

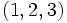
Les quartiles suivants contiennent les 25% d'observations suivantes

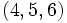
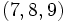
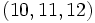
En tant que valeurs, les trois quartiles sont Q1 = 3,75, Q2 = 6,5 qui est par ailleurs la médiane, et Q3 = 9,25.

L'écart interquartile est alors simplement la différence entre Q3 - Q1, soit ici 9,25-3,75 = 5,5.

Si nous l'interprétons en termes d'étendue, l'écart interquartile correspond à un ensemble de valeurs autour de la médiane tel qu'il contient les 50% d'observations les moins extrêmes. Le mode de calcul de l'espace interquartile n'est d'ailleurs qu'un cas particulier d'opération utilisant des distributions tronquées, c'est-à-dire de distribution dont on a retiré les valeurs les plus extrêmes.