Statistique descriptive
Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Rédaction : Éric Raufaste
4. Représentations graphique des distributions
4.2. Distributions observées, cas discret
2.1. Histogrammes
Si les valeurs sont discrètes, la solution est immédiate : il suffit de tracer un histogramme en prenant les modalités de la variable pour l'axe des X, et l'effectif dans chaque modalité sur l'axe des Y, et le tour est joué. Rappelons qu'un histogramme est un mode de représentation graphique qui met en relation une (ou plusieurs) variables discrètes (par exemple des catégories, des classes ordinales, ou des intervalles numériques disjoints) et une variable numérique. En voici un exemple :
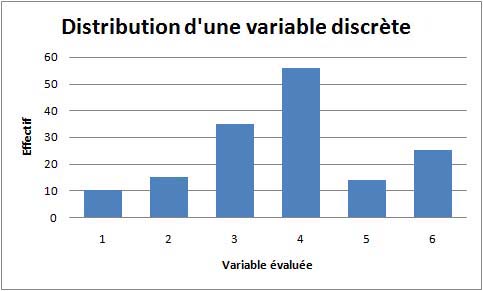
Bien que claire, la représentation précédente présente une particularité, qui pourra s'avérer importante selon l'usage qui est visé pour la représentation de la distribution. S'il s'agit de comparer deux distributions ayant le même effectif et le même nombre de modalités, et si l'on a pris soin de garder la même échelle pour l'axe des Y, alors pas de problèmes, les deux graphiques seront directement comparables. Mais si les deux distributions à comparer ont des effectifs très différents (par exemple, on veut comparer la distribution obtenue sur l'ensemble de la population française avec ce qui a été obtenu sur un échantillon donné représentant, disons, 60000 fois moins d'observations), la comparaison directe ne sera plus possible. Il sera alors plus avantageux de remplacer les effectifs bruts dans chaque modalité par le pourcentage d'observations qui tombent dans chaque modalité. Ainsi les deux histogrammes deviennent comparables. Par exemple :
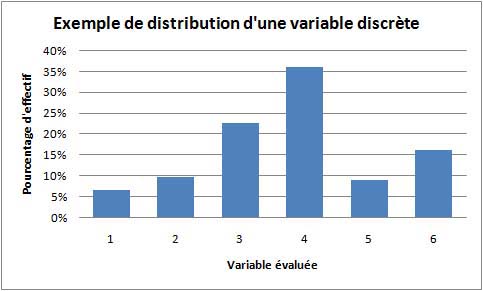
Sur cet exemple, on voit bien que la forme n'a pas changé, mais l'axe des Y est maintenant exprimé avec des pourcentages et deux distributions d'effectifs bruts très différents deviendraient comparables.
2.2. Les boîtes à moustaches (ou «Boxplots»)
Les boîtes à moustaches sont une représentation de la distribution d'une variable qui repose sur cinq valeurs. Le rectangle central représente le gros de la distribution, avec la valeur centrale, généralement la médiane, marquée ici par une ligne. Les petits traits placés aux extrémités indiquent les bornes extérieures de la distribution. Toutefois, selon le paramétrage du logiciel, ces valeurs peuvent correspondre à des fonctions différentes.
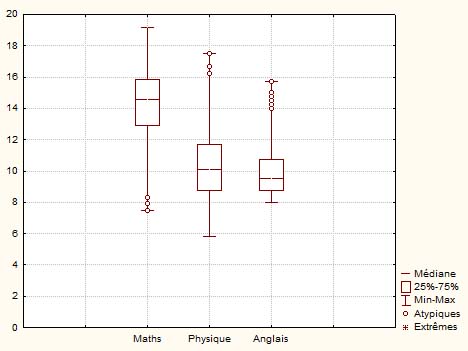
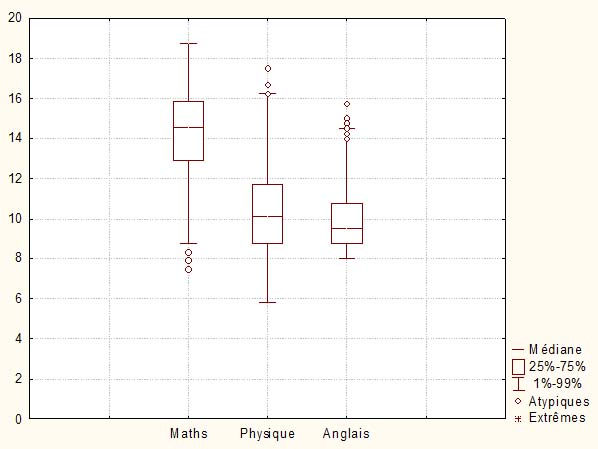
Dans ce premier exemple, où est représentée une distribution des trois notes sur 20 obtenues par 500 étudiants à un concours écrit d'entrée dans une grande école, avec une épreuve de maths, une épreuve de physique et une épreuve d'anglais, on a une boîte à moustache par note. Les cinq valeurs considérées sont le Min et le Max pour les extrémités, et les trois quartiles pour le rectangle central. Les quartiles Q1 et Q3 délimitent le rectangle central qui, de ce fait, représente directement l'écart interquartile. La médiane (= quartile Q2) est la ligne interne au rectangle. Les points vers les extrémités représentent des valeurs extrêmes, c'est-à-dire des notes qui se démarquent sensiblement des notes obtenues par le reste des candidats.
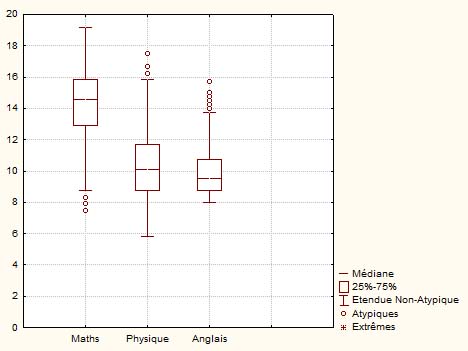
Dans ce second exemple, les trois mêmes distributions sont représentées par des boîtes à moustaches mais les valeurs extrêmes sont maintenant les valeurs considérées comme correspondant à l'étendue des valeurs non-atypiques. De ce fait, les valeurs extrêmes marquées par les petits cercles se retrouvent en dehors de cette étendue.
Nous terminerons par un troisième exemple dans lequel les valeurs marquant les extrémités des moustaches sont définies par le premier et le 99ème percentile. Autrement dit, les notes telles que 1% des notes sont plus petites que la moustache basse, et 1% des notes sont plus hautes que la moustache haute.
2.3. Diagrammes à secteurs "Camemberts"
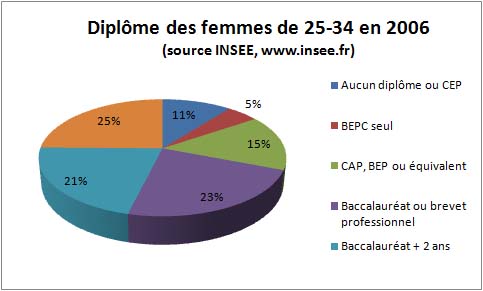
Lorsqu'il s'agit de représenter les effectifs par modalités d'une variable discrète, une représentation très commune est le diagramme à secteurs ou « camembert », par analogie évidente avec la forme usuelle de la boîte du fromage éponyme.
Voici un exemple :
