UOH / Statistique et Psychométrie en L1

Tout d'abord, commençons par remarquer que parler de valeurs continues pour des données d'observations est en réalité un abus de langage. En effet, mathématiquement une variable est continue si quelles que soient deux valeurs de cette variable, on peut toujours avoir une troisième valeur qui vient s'intercaler entre elles. Par exemple, entre 2,3 et 2,4 on peut placer 2,35. Entre 0,000000001 et p 0,000000002, on peut placer p 0,0000000015. Et ainsi de suite à l'infini. Parler de valeurs continues pour une variable observée signifie donc que l'on serait capable de discriminer entre deux valeurs infiniment proches.p Mais absolument p aucun instrument de mesure ne dispose d'une précision infinie. Donc quand on parle de valeurs observées sur une dimension continue, en réalité, on dit simplement que notre dispositif de mesure permet suffisamment de finesse pour nous donner l'impression de continuité. p Un peu de la même façon que les pixels sur un écran d'ordinateur sont suffisamment proches les uns des autres pour nous donner l'illusion de continuité de l'image alors qu'en réalité les pixels sont bien séparés les uns des autres. Ou encore comme lorsque au cinéma, nous avons l'impression d'un mouvement fluide et continu alors qu'il ne s'agit que d'une série rapidement diffusée d'images nettement séparées. Toutes les données d'observation ne sont en réalité que fictivement continues, même en supposant que la variable théorique qu'elles sont censées mesurer soit, elle, continue. p

Une fois admis ce principe, on est fondé à utiliser la technique de l'histogramme pour représenter n'importe quelle distribution, que la variable observée soit discrète ou pseudo-continue.

La solution technique pour construire l'histogramme consiste à découper l'axe des p X p en intervalles, et à regrouper pour les compter ensemble toutes les observations qui tombent dans cet intervalle. On va ainsi obtenir un tableau avec, pour chaque valeur, le nombre d'observations associées. À partir de là, il ne restera plus qu'à tracer l'histogramme correspondant. Cet histogramme sera alors la représentation graphique de l'échantillon. Et dans la mesure où l'échantillon est la meilleure estimation de la population cible, il constitue par là même une représentation de la distribution de la population cible. Ce n'est évidemment pas la seule possible. Il suffit d'avoir un autre échantillon, plus large et/ou plus représentatif de la population cible pour pouvoir en extraire une meilleure représentation de la distribution cible.p

Dans l'exemple de la figure qui suit, les valeurs portées sur l'axe des axes sont liées à une variable calculée, et le mode de calcul fait que cette variable était donné avec 7 décimales après la virgule. Nous avons donc là une précision des données exagérées (ne correspondant pas à la vérité de ce que nous étions capables de mesurer effectivement), et en tout cas suffisamment élevée pour que cela représente un nombre de modalités considérable, largement supérieur au nombre d'observations disponibles. Nous sommes donc dans un cas où il faut construire des intervalles permettant d'agréger les observations. Ici, il a été demandé au logiciel de construire 13 intervalles. Le logiciel de statistiques a donc découpé l'étendue des observations (i.e., la différence entre la plus grande et la plus petite valeur) entre 13 intervalles de taille égale, et a compté combien d'observations tombaient dans chacun des 13 intervalles. La courbe en rouge a été ajoutée par le logiciel pour indiquer ce que serait la distribution théorique si ces données correspondaient à une distribution normale. On peut donc avoir une impression visuelle de la normalité (ou non) des données issues de l'échantillon.p

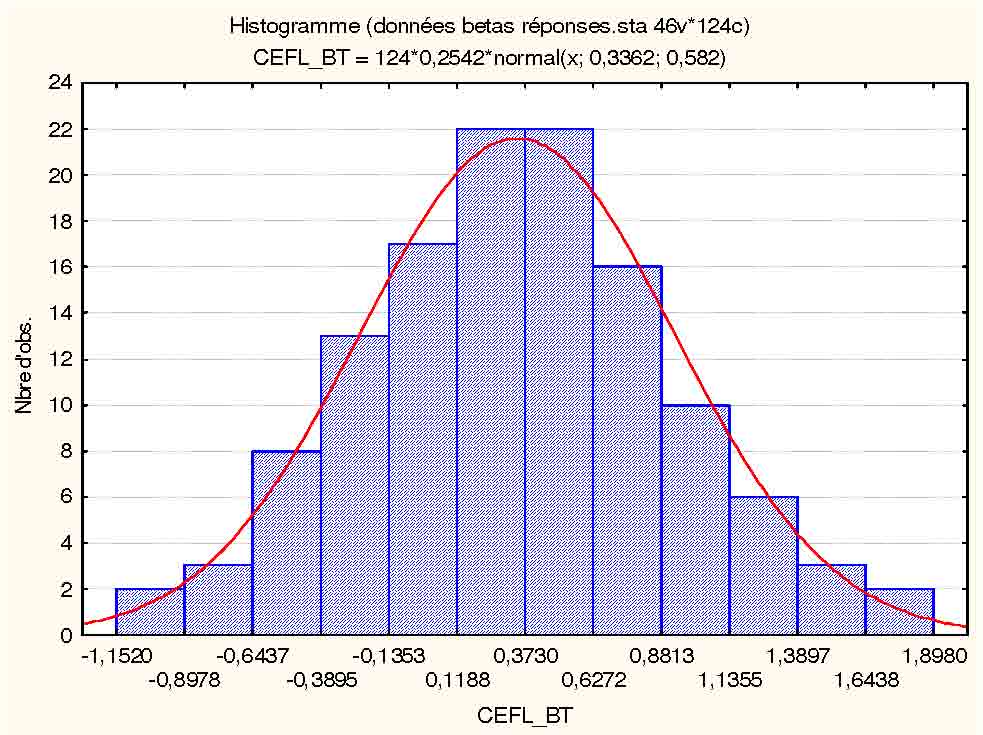
Remarquons que la taille des intervalles peut varier, puisqu'elle dépend du nombre d'intervalles qu'on choisit de prendre. C'est un choix de la part de la personne qui construit la représentation. On remarquera alors que selon le choix de la taille des intervalles, la distribution peut parfois changer de forme. Au minimum, on prendra des intervalles correspondant à la précision de notre dispositif de mesure puisque de toute façon, des intervalles plus fins n'auraient aucun sens. En revanche, on peut être amené à faire des regroupements plus larges. En effet, p toutes choses égales par ailleurs, plus l'on prend des intervalles fins et plus le nombre d'observations dans chaque intervalle sera petit. À la limite, on risque de retomber sur le problème qu'on aurait avec de vraies variables continues, à savoir une seule observation dans quelques intervalles et aucune observation dans la plupart des intervalles. Un histogramme quasiment plat en quelque sorte, donc très peu informatif. Une solution naturelle consiste alors à choisir des intervalles plus larges, donc moins nombreux, mais contenant plus d'observations. Il n'y a pas de règle de choix stricte. Le choix de la bonne taille d'intervalles est affaire d'intuition du chercheur, en fonction de ce qu'il veut montrer et en fonction des propriétés des données dont il dispose.