Statistique descriptive
Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Rédaction : Éric Raufaste
5. Quelques distributions statistiques remarquables
5.2. La distribution normale
Si l'on prend un mètre et que l'on mesure la taille d'un enfant, on obtient une valeur. Si l'on refait la mesure, on obtiendra une valeur peut-être identique, mais le plus souvent très légèrement différente. De ce fait, répéter l'opération de mesure permettra de construire une distribution. Depuis au moins Laplace, une question cruciale pour les scientifiques confrontés à l'imprécision et aux petites fluctuations aléatoires des mesures était de comprendre les propriétés mathématiques de cette distribution. En effet, en comparant les propriétés mathématiques d'une distribution donnée aux propriétés mathématique d'une distribution purement due à de petites fluctuations aléatoires, on peut évaluer si la distribution obtenue est biaisée, ou sous l'influence d'un facteur systématique quelconque, ou encore purement explicable par le hasard.
La distribution normale est celle qui traduit la répartition de mesures qui sont entachées d'une somme de multiples petites fluctuations aléatoires, fluctuations qui se produisent inévitablement lorsque l'on mesure une grandeur dans l'univers physique. Cette distribution apparaît dès que certaines conditions très banales sont réunies. L'une de ces conditions est l'existence d'une régression à la moyenne, c'est-à-dire que suite à l'observation de valeurs extrêmes, les valeurs suivantes tendent à revenir vers la moyenne. Il ne s'agit toutefois que d'une tendance et non quelque chose de systématique.
Un exemple de régression à la moyenne est le QI intergénérationnel. La régression à la moyenne en ce cas tient à ce que la moyenne des QI des enfants tend à être 20% plus proche de la moyenne générale de la population (100) que la moyenne des QI des parents. Si le père à un QI de 140 et la mère un QI de 140, leur moyenne fait 140 et le plus probable est que le QI moyen de leurs enfants tourne autour de 132. Il reste bien entendu possible dans certains cas que les enfants de parents dont le QI moyen est 140 aient un QI plus élevé que 132, voire même que 140, mais cela arrivera plus rarement que le contraire. La principale seule raison pour laquelle tout le monde n'a pas exactement 100 au bout de quelques siècles, c'est que la transmission génétique et l'effet de l'environnement où l'enfant grandit possèdent un caractère aléatoire qui fait qu'émergent spontanément des enfants avec des valeurs plus extrêmes que celles de leurs parents. Il reste qu'un très bon prédicteur du QI des enfants est celui des parents, et que ces conditions suffisent à assurer une distribution normale.
Cette distribution théorique est très connue. En voici un exemple :
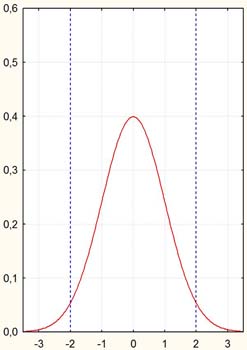
Dans cet exemple, on a représenté une distribution normale de notes dont la moyenne vaut 0 et l'écart-type vaut 1.
Dans la simulation suivante, vous avez la possibilité de faire varier les paramètres de la distribution normale (moyenne et écart-type), puis cliquez sur "Tracez" pour voir directement comment cela affecte la forme de la distribution. À chaque essai, une nouvelle courbe s'ajoutera sur le graphique. Cliquez sur le bouton « Effacez » pour réinitialiser la page. Veuillez noter que l'échelle choisie pour l'axe vertical est plus petite que sur le graphique précédent, ce qui permet de représenter une plus grande diversité de courbes, mais si vous tracez la courbe de moyenne 0 et d'écart-type 1, elle semblera plus aplatie que sur le graphique précédent.
On peut voir sur cette courbe plusieurs propriétés classiques des distributions normales : le pic de fréquence correspond à la note moyenne, la distribution est symétrique autour de cette moyenne, et enfin les valeurs extrêmes correspondent à une raréfaction croissante des observations : plus on s'éloigne de la moyenne, d'une côté comme de l'autre, et plus la fréquence tend vers 0.
Cette distribution s'applique par exemple à la taille des français ou aux notes de QI que l'on peut observer dans une population d'enfants ou d'adultes. Voici quelques propriétés utiles à connaître.
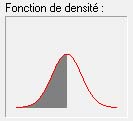
50% des observations sont inférieures à la moyenne et 50% au-dessus. Par exemple, environ 50% des individus ont un QI entre 0 et 100 (zone grisée) et 50% un QI plus haut que 100 (zone non grisée).
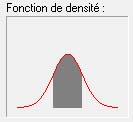
68% des observations tombent entre -1 et +1 écart-type de distance à la moyenne. Par exemple, 68% des individus ont un QI entre 85 et 115 (zone grisée).
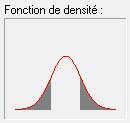
Réciproquement, les 32% d'individus restant sont à plus d'1 écart-type de distance, par défaut (zone grisée à gauche) ou par excès (zone grisée à droite), soit, en termes de QI, à moins de 85 ou à plus de 115.
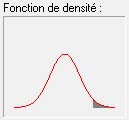
Si l'on prend 2 écarts-types, c'est 95% des observations qui tombent dans l'intervalle [m-1 écart-type; m+1 écart-type]. D'où moins de 2,5% d'individus ayant un QI plus grand que 130 (zone grisée à droite).
On peut aussi raisonner dans l'autre sens.
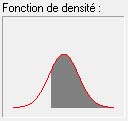
Prenons par exemple une mesure politique visant à amener 80% d'une classe d'âge au bac. Connaissant la distribution du QI, imaginons qu'on amène au bac tous les individus ayant le QI le plus haut (ce qui n'est évidemment pas le cas puisque de nombreux surdoués sont en échec scolaire). Cela correspond à la zone grisée du graphique. On voit alors que l'on donnera le bac à des individus dont le QI sera d'environ 88.