Statistique descriptive
Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Rédaction : Éric Raufaste
6. Techniques de recodage des données
6.3. La centration-réduction
3.1. Pourquoi centrer-réduire ?
Le principal avantage de la centration-réduction est de rendre comparables des variables qui ne le seraient pas directement parce qu'elles ont des moyennes et/ou des variances trop différentes.
Un autre avantage, mais qui dépasse le niveau du présent cours, est relatif à la régression à plusieurs prédicteurs, lorsque l'on envisage d'étudier les interactions entre VI. Dans ce cas, il est conseillé de commencer par centrer-réduire les prédicteurs avant de calculer les termes d'interaction.
3.2. Qu'est-ce que la centration ?
On appelle centration l'opération qui consiste à retirer de chaque valeur d'une variable la moyenne de la variable.
Imaginez une variable normale de moyenne m et d'écart-type s. Si à chacune des valeurs de la variable, on retire la valeur constante m, on obtient une nouvelle variable qui, par les propriétés de la moyenne, aura pour moyenne 0. Son écart-type, par contre, vaudra toujours s.
3.3. Qu'est-ce que la réduction ?
On appelle réduction l'opération qui consiste à diviser chaque valeur d'une variable par l'écart-type de la variable.
Imaginez une variable normale de moyenne m et d'écart-type s. Si on divise chacune des valeurs de la variable par la constante s, on obtient une nouvelle variable qui, par les propriétés de la moyenne, aura pour moyenne m / s et pour écart-type 1.
Une autre propriété importante de la réduction est d'éliminer l'unité de la variable. Par exemple, si la variable est une taille, disons en mètres, alors l'unité de l'écart-type est aussi en mètres. Du coup, en divisant des mètres par des mètres, on obtient un nombre sans unité. De ce fait, s'il devient possible de comparer les dispersions de deux variables alors même qu'elles n'étaient pas initialement mesurées avec les mêmes unités.
3.3. Qu'est-ce que la centration-réduction ?
C'est tout simplement l'application combinée d'une centration puis d'une réduction. Ainsi, à chaque valeur Xi on fera correspondre une valeur dite centrée-réduite, que l'on note usuellement par la lettre Z :
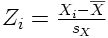
La distribution ainsi obtenue aura pour moyenne 0 et pour écart-type 1. Chaque note représentera directement une distance à la moyenne exprimée en écarts-types. Par exemple, une valeur de -3,2 signifie que pour cet individu la valeur mesurée était 3,2 écarts-types plus bas que la moyenne.
Notons que la plupart des logiciels de statistique, comme par exemple R, jamovi ou Statistica, fournissent des fonctions qui opèrent directement une centration-réduction sur les variables que vous leur indiquez.