Statistique descriptive
Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Rédaction : Éric Raufaste
6. Techniques de recodage des données
6.4. La répartition en classes sur la base des effectifs
L'idée générale de la répartition en classes est que l'information portée par les nombres initiaux est inadéquatement riche (i.e., elle porte plus de bruit que d'information réelle). Toutefois, la logique de classification n'est pas du tout la même selon qu'on cherche à produire des classes sur la base des effectifs qu'elles contiendront, ou sur la base de leurs propriétés propres.
4.1. Répartition en classes d'effectif égal
Une catégorisation simple consiste à déterminer plusieurs classes d'effectif égal. En général, ce genre de classification est opérée sur la base d'une variable au moins ordinale (c'est-à-dire telle que les valeurs qu'elle prend respectent une relation d'ordre). La première opération est alors de reclasser les sujets selon leur rang sur la variable considérée (ce qui revient à faire un tri à plat). On découpe alors les classes selon le nombre souhaité, soit 1/ k sujets par classe lorsqu'il y a k classes. Cette opération s'appelle le quantilage et les limites de classes des quantiles. S'il y a dix classes, on parle alors de déciles. S'il y en a 4, on parle de quartiles. Cette procédure et ces termes avaient déjà été détaillés dans l'article sur les dispersions de variables ordinales.
Avec deux classes, cela donne 1/2=50% de sujets par classes. Ainsi, par exemple, on peut distinguer le groupe des valeurs fortes et des valeurs faibles en partitionnant la variable selon la médiane. Les 50% de sujets dont la valeur est supérieure ou égale à la médiane (par exemple) reçoivent une valeur arbitraire, disons 1, et les 50% restants reçoivent une autre valeur, disons 0.
Si l'on a des raisons de penser qu'une classification à 3 niveaux serait plus appropriée, il faut donc diviser les sujets en trois classes représentant chacune 33% de sujets, par exemple les sujets faibles, moyens et forts.
Et ainsi de suite en fonction du nombre de classes désiré.
4.2. Répartition en classes normalisées : la normalisation
Dans certains cas, on peut avoir besoin que les différentes classes possèdent une répartition à peu près normale, au sens où l'on trouve une proportion d'individus dans chaque classe sensiblement équivalente à ce que donnerait une distribution normale. Comme dans le cas de la classification en classes égales, tout commence par un tri à plat , c'est-à-dire que la première opération consiste à ranger les sujets par ordre croissant (ou décroissant, au choix) selon la variable considérée.
Connaissant la loi normale et connaissant le nombre de classes souhaitée, on peut alors déterminer les effectifs de chaque modalité. Par construction de la loi normale, et connaissant la moyenne et l'écart-type d'une distribution normale (c'est-à-dire connaissant ses paramètres), on sait quelle est la proportion d'effectifs compris entre telle et telle valeur. Par exemple, si la moyenne est 0 et l'écart-type 1, alors 68% des observations seront comprises entre les valeurs -1 et +1. En procédant dans l'autre sens, on peut mettre le pourcentage souhaité d'individus dans chaque classe. Ainsi, selon une technique nommée STANINE qui s'utilise dans certains tests, et notamment dans les tests psychotechniques utilisés en navigation aérienne depuis la seconde guerre mondiale, on classe les sujets en neuf classes selon leur performance. La logique est la suivante : Chaque classe couvre un demi-écart-type et la classe centrale, la classe 5, a pour centre la moyenne de la distribution. La classe 5 comprend donc tous les sujets qui ont une note comprise entre la moyenne -0.25 écart-type et +0,25 écart-type. La classe 4 comprend donc tous les sujets qui ont une note entre -0.75 écart-type et -0.25 écart-type. Par définition de la loi normale standard, on sait alors que la classe 1 doit contenir 4% de sujets, les 4% de sujets les plus faibles. La classe 2 doit contenir les 7% de sujets suivants, et ainsi de suite : 12% pour la classe 3; 17% pour la classe 4, 20% pour la classe 5; 17%; pour la classe 6; 12% pour la classe 7; 7% pour la classe 8; et enfin les 4% les plus forts reçoivent la classe 9. La distribution ainsi obtenue apparaît dans le graphique suivant :
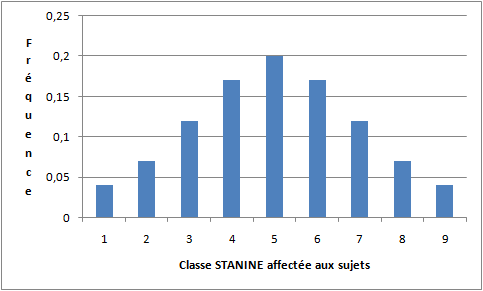
Comme vous le voyez, en procédant ainsi, on obtient une distribution d'allure normale même si les sujets n'avaient pas fourni des notes distribuées normalement à la base.
Par contre, cet avantage évident est compensé par des inconvénients qu'il ne faut pas se cacher. Par exemple, deux sujets ayant fourni des performances extrêmement similaires peuvent, par le seul jeu du recodage, se trouver classés dans des classes différentes. Réciproquement, tous les sujets d'une même classe se retrouvent avec la même note, celle de leur classe. De ce fait, le recodage ainsi réalisé produit des effets de bord non négligeable puisque deux sujets ayant fourni presque la même (voire la même) performance peuvent avoir des notes différentes alors que deux sujets ayant produit des performances assez dissemblables peuvent finalement se trouver avec la même note.