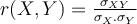UOH / Statistique et Psychométrie en L1

3.1. Définition

Le principal problème de la covariance, c'est que si on multiplie une des deux variables par deux (exemple précédent), la covariation des deux variables n'est pas affectée et pourtant la covariance elle-est affectée. Pour éviter cet effet, il faut standardiser la covariance en la divisant par la dispersion de chacune de deux variables. On obtient ainsi ce qu'on appelle le coefficient de corrélation linéaire :

$r(X,Y)=\frac{\sigma_{XY}}{\sigma_X.\sigma_Y}$

En France, on l'appelle aussi coefficient de Bravais-Pearson, mais à l'étranger il est seulement connu sous le nom de coefficient de Pearson... et son origine est à chercher chez Francis Galton. 

3.2. Propriétés remarquables et interprétation

3.2.1. Valeurs prises par le coefficient de corrélation

Le coefficient de corrélation varie entre -1 et +1, indépendamment des échelles des variables 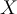$X$ et $Y$.

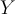La valeur +1 traduit une corrélation linéaire positive parfaite, c'est-à-dire que toute variation d'une variable se traduit par une variation proportionnelle et de même direction sur l'autre variable.

La valeur -1 traduit une corrélation linéaire négative parfaite, c'est-à-dire que toute variation d'une variable se traduit par une variation proportionnelle et de direction inverse sur l'autre variable (si l'une monte, l'autre descend).

La valeur 0 signifie l'absence de corrélation linéaire (mais pas forcément l'absence de relation)

3.2.2. Chausse-trappe n°1 : corrélation n'est pas causalité !

Une erreur fréquente chez les débutants consiste à confondre corrélation et causalité : ce n'est pas parce que deux variables sont très liées (i.e., qu'elles corrèlent à +1 ou -1) que l'une est la cause de l'autre. Plusieurs possibilités différentes peuvent expliquer une corrélation très forte. Parmi ces possibilités, deux sont notables :

1°) l'effet du hasard : il est toujours possible qu'une corrélation observée très forte soit entièrement due au hasard. Il existe des techniques pour évaluer ce risque, mais elles ne sont pas au programme de ce cours.

2°) l'effet d'une troisième variable cachée. Supposons par exemple que l'on découvre une corrélation très forte entre la couleur des dents et le cancer du poumon. Serait-il raisonnable de penser que les dents jaunes causent le cancer du poumon ? Ou que le cancer du poumon fait jaunir les dents ? En fait, il existe une troisième explication : la consommation de tabac fait jaunir les dents ET cause le cancer du poumon.

3.2.3. Chausse-trappe n°2 : absence de corrélation linéaire n'est pas absence de liaison !

En présence d'une corrélation nulle, on pourrait être tenté de se dire qu'il n'y a pas du tout de relation entre les deux variables. Si cette possibilité existe, elle est néanmoins loin d'être la seule. En effet, le mode de calcul de la corrélation linéaire fait que ce coefficient détectera une liaison dans le cas où la forme de la relation est une droite, ou suffisamment proche d'une droite (d'où l'expression de corrélation linéaire).

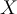La figure ci-dessous, par exemple, représente la parabole d'équation $Y=X^2$. Autrement, à toute valeur de $X$, on fait correspondre la valeur 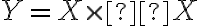$Y = X\times X$. La liaison est évidemment parfaite puisqu'on sait précisément quelle sera la valeur de 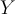$Y$ dès qu'on connait la valeur de $X$.

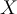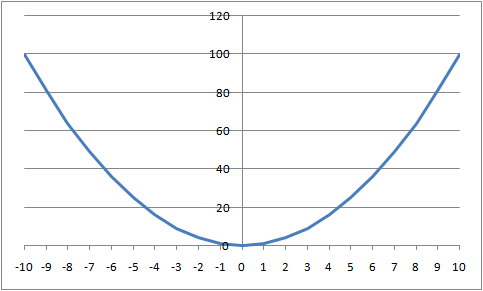
Or, le coefficient de corrélation sera alors de zéro ! En effet, le coefficient de corrélation mesure à quel degré toute augmentation sur une variable se traduit de manière régulière par un accroissement (ou une décroissance) proportionnelle sur l'autre variable. Si l'on a une parabole par exemple, les accroissements sur 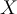$X$ vont se traduire d'abord par une décroissance sur 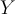$Y$ (voir figure plus haut), puis dans un second temps par une augmentation sur 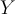$Y$ ! Au total, il y aura eu autant d'accroissements que de décroissance et le coefficient de corrélation sera annulé alors même que la dépendance était parfaite : connaissant une valeur de 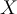$X$, on pouvait prédire parfaitement la valeur que prendrait $Y$.

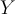3.3. Stratégie de calcul

Vous pouvez trouver une démonstration d'une méthode simple pour le calculer, dans la section savoir-faire du présent cours, qui présente comment utiliser le tableur OpenOffice avec la fonction PEARSON().