Statistique descriptive
Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Rédaction : Éric Raufaste
9. Prédire une variable numérique : la régression simple
9.2. Notion de courbe de régression
A. Le nuage de points
Dans le cas le plus général, on pourrait souhaiter prédire plusieurs variables à partir de plusieurs prédicteurs et avec des relations mathématiques de toutes sortes entre les prédicteurs et les variables à prédire. Toutefois, au niveau d'un cours de L1, il est préférable de commencer par le cas le plus simple, dans lequel il n'y a qu'une variable à prédire et qu'un prédicteur, et dans lequel la nature de la relation est une relation affine. Autrement dit, nous nous plaçons dans le cas de la régression linéaire simple.
La figure ci-dessous représente un tel nuage de points réalisé à partir de 242 observations avec une variable à prédire qui varie entre -10 et 10, et un prédicteur qui varie entre 0 et 8. Attention au fait qu'il n’y a pas 242 points sur le graphique, car plusieurs observations peuvent correspondre à un même point.
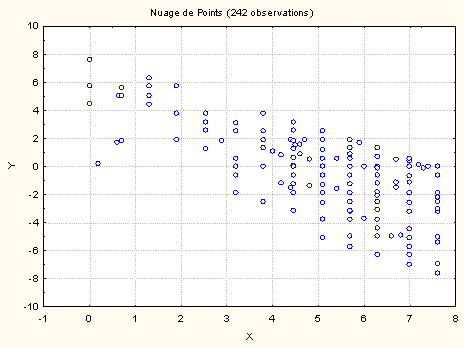
S'il y a une relation entre X et Y, cela signifie que les valeurs de Y sont déterminées par les valeurs de X, aux erreurs de mesure près. Notons que, dans le cas général, la relation pourrait aussi bien être dans l'autre sens, à savoir que les valeurs de X soient déterminées par celles de Y. À l'inverse, nous avions vu dans l'article précédent, sur la corrélation, que l'on peut définir l'absence de relation comme étant le fait que les valeurs d'une variable ne sont pas affectées par les valeurs prises par l'autre variable. Autrement dit, quelle que soit la valeur Xi considérée, la distribution des valeurs de Y autour de Xi sera la même. Graphiquement parlant, le nuage de points ressemblera alors à un rectangle horizontal. Ici, on n'a pas l'impression d'un rectangle et on a l'impression d'une pente décroissante (on descend en allant vers la droite). La forme du nuage de points nous indique donc que l'idée d'une relation entre les deux variables n'est pas a priori saugrenue : il semble que les valeurs de Y ne soient pas distribuées au hasard selon les valeurs de X. La question qui se pose alors à nous est d'essayer d'analyse quelle pourrait être cette relation.
Pour cela, nous allons essayer de définir un peu plus précisément l'intuition que nous donne la vue du nuage de points. Il nous faut donc un concept qui permette de traduire un peu plus formellement l'idée que les valeurs d'une variable sont -- ou non -- distribuées de façon équivalente selon les valeurs de l'autre variable.
Un premier pas est de définir les notions de moyenne et variance conditionnelles.
B. Moyenne et variance conditionnelles
Si je considère une valeur donnée de X, disons par exemple 0 sur le graphique ci-dessus. Je vois pour cette valeur de X là, Y a pris trois valeurs, c'est-à-dire que l'on a trouvé des individus ayant obtenu 0 sur la variable X , mais ayant obtenu des valeurs différentes sur la variable Y. Du coup, il est possible de calculer la moyenne des valeurs de Y qui correspondent à chaque valeur particulière de X. C'est ce que l'on appelle la moyenne de Y conditionnelle à X. De la même manière, on peut calculer une variance de Y conditionnelle à X. Réciproquement, on pourrait s'intéresser aux valeurs que prend X pour une valeur de Y donnée. Cela nous permettra de calculer une moyenne de X conditionnelle à Y et une variance de X conditionnelle à Y.
C. Courbes de régression
Si l’on trace pour chaque valeur de X, le point correspondant à la moyenne des valeurs Y en cette valeur de X, les moyennes de Y conditionnelles en X donc, et que l’on joint ensuite ces points, on obtient une courbe dite courbe de régression de Y en X (voir figure ci-dessous). Si l'on imagine que X prédit parfaitement Y, alors la valeur moyenne de Y conditionnelle en chaque point de X devrait être la valeur prédite par la relation. Et par conséquent, la courbe de régression serait en fait la courbe qui exprime la relation entre X et Y. En pratique toutefois, les mesures empiriques sont toujours entachées de bruit, de sorte qu'il existe toujours une certaine quantité de variations autour de la moyenne conditionnelle (autrement dit, la variance conditionnelle n'est jamais nulle).
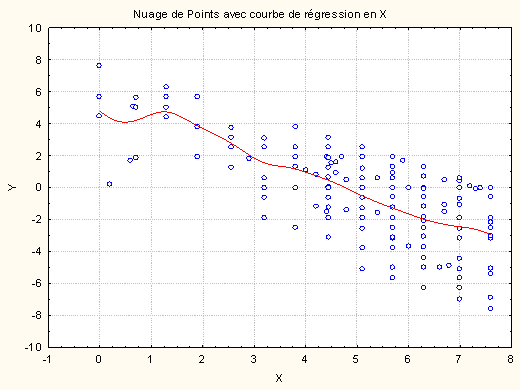
Dans l’exemple de la figure ci-dessus, la courbe de régression ne passe pas nécessairement au milieu des points d’une verticale donnée. Cela s’explique par le fait que chaque point est pondéré par le nombre d’observations correspondant. Un point présent dans beaucoup d’observations va donc plus « attirer » la courbe de régression que les autres points.
Réciproquement, on peut tracer la courbe de régression de X en Y et cette courbe de régression représente la meilleure estimation possible de la capacité de Y à prédire X.
Pour chaque point du nuage, sa coordonnée Yi (resp. Xi) peut se décomposer en une partie correspondant à la courbe de régression en X (resp. Y) plus une partie résiduelle. Exprimé en termes de variance, cela donne
Var (Y) = variance « expliquée par la courbe de régression » en X + Variance résiduelle
Ou encore
Var (X) = variance « expliquée par la courbe de régression » en Y + Variance résiduelle