Statistique descriptive
Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Rédaction : Éric Raufaste
9. Prédire une variable numérique : la régression simple
9.3. Ajustement des courbes de régression
Lorsque l’on veut modéliser les données, la question qui se pose ensuite est de trouver l’équation des courbes de régression. Les courbes de régression correspondent généralement à des fonctions compliquées, mais on peut chercher à les approcher par des fonctions plus simples. Le principe général est de partir d’une forme de fonction connue et de chercher les paramètres qui ajustent le mieux possible les courbes obtenues aux courbes de régression.
Par exemple, si l'on part de l'idée que la courbe de régression, si l'on mettait de côté les erreurs de mesure, serait une droite, alors elle serait caractérisée par une équation de type
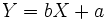
Il faudrait alors identifier les paramètres a et b pour connaître l'équation de la droite.
Si l'on imagine que la courbe de régression correspond à une parabole, l'équation cherchée serait de la forme :
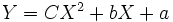
et dans ce cas, il faudrait trouver les valeurs des trois paramètres, a, b, et c.
L'idée générale pour identifier les paramètres est d'ajuster les valeurs des différents paramètres pour que l'erreur commise en appliquant l'équation obtenue soit minimale. Par exemple, imaginons qu'on décide que la courbe de régression de la figure précédente correspond en réalité à une droite et que cette droite a pour paramètre b =-0.5 et a =+4. Pour chaque individu i, on est alors en mesure de calculer pour chaque valeur de X la valeur de Y prédite par cette droite. On note cette valeur (prononcer « Y chapeau »)
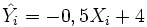
Maintenant, du fait de l'erreur de mesure, pour chaque observation une erreur de prédiction est commise, erreur appelée résidu et directement mesurable par l'écart entre la valeur prédite et la valeur observée :p
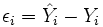
Finalement, l'idée de l'ajustement est de retenir le jeu de paramètres tel que l'erreur ε moyenne sera minimale. Dans le cas de la régression linéaire, on s'appuie sur l'idée d'une droite et donc le jeu de paramètres à trouver est le jeu des valeurs p a et b qui minimisent la fonction d'erreur. On emploie alors le terme de"droite de régression" pour décrire la fonction qui approxime la courbe de régression. Dans le cas particulier du nuage de points précédent, les paramètres optimaux sont b =-1,15 et a =5,4 :
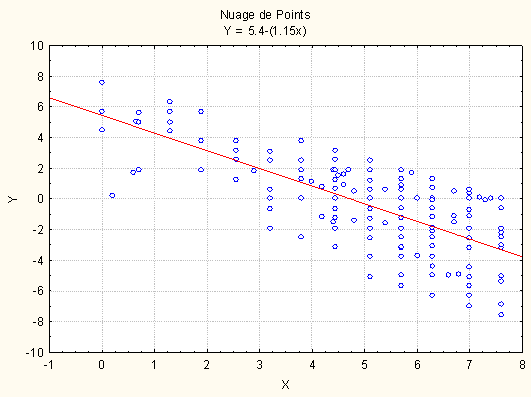
Dans le cas de la régression, il se trouve que des relations mathématiques relativement simples permettent de trouver d'emblée les paramètres qui minimisent la fonction d'erreur. Ainsi, la pente de la droite de régression en X est donnée directement par la formule suivante :
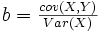
De la même façon, la pente de la droite de régression en Y est donnée par la formule
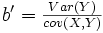
Les paramètres restants correspondent aux intercepts, c'est-à-dire à la valeur de Y quand X vaut 0 et à la valeur de X quand Y vaut 0. Sachant que les deux droites de régression passent par le centre de gravité G du nuage de points et que ce dernier a pour coordonnées
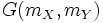
il est facile de dériver les intercepts.
Mais de toute façon, même si vous ne maîtrisez pas les mathématiques pour réaliser vous-mêmes ces calculs, pers logiciels le font très bien et de nos jours, on peut très bien faire des régressions sans réaliser un seul calcul soi-même. L'important est de comprendre la logique du processus. Un exemple de calcul détaillé sera présenté dans la rubrique "Zoom sur..."
Il reste maintenant à évaluer la qualité de l'ajustement produit. Cela est réalisé très simplement en calculant la corrélation entre les valeurs prédites par le modèle et les valeurs observées :
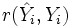
L'idée est que si la prédiction est parfaite, la corrélation sera de 1.
On peut alors montrer que la part de variance expliquée par le modèle est donnée directement par le carré de la corrélation précédente. Une valeur de r à 0.5 signifie alors que le modèle explique 0.5*0,5=25% de la variance.