Échelles de mesure (Tout est-il mesurable ? )
Objectifs : Définir le concept d'échelle de mesure et donner les éléments critiques nécessaires à son utilisation.
Prérequis :
- Application
- Loi normale
- Mesure, mesurage et codage numérique
- Relation d'équivalence
- Relation d'ordre et ordre partiel
- Relations entre Statistique et Psychométrie
Résumé : en Psychologie et plus généralement en Sciences Humaines et Sociales, les phénomènes auxquels on s'intéresse "n'émanent pas" de grandeurs mesurables, c'est-à-dire de grandeurs possédant des unités de mesure empiriquement définies. Les phénomènes se laissent plus naturellement décrire en termes de classifications et d'ordres partiels. Nombre d'applications psychologiques reposent sur des ordres considérés comme totaux, par approximation ou par convention, ainsi que sur la définition de distances conventionnelles relatives à des grandeurs hypothétiques. Ces trois approches, (i) classification, (ii) ordre total et (iii) distances, sont associées à ce que l'on appelle, après Stevens (1946), les échelles (i) nominale, (ii) ordinale et (iii) d'intervalle. Les échelles dites de ratio correspondent au mesurage au sens classique du terme. Une utilisation rigoureuse des échelles de mesure nécessite d'expliciter en quoi les codages associés à ces échelles représentent des opérations sur les objets faisant l'objet de l'échelonnement.
rédaction : Stéphane Vautier, 5 pages plus un test d'auto-évaluation final.
2. Échelle nominale et classification
L'échelonnement des objets d'un ensemble E sur une échelle nominale repose sur l'établissement d'une relation d'équivalence sur les éléments de cet ensemble E. Autrement dit, pour tout couple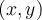 
d'éléments de E, il faut pouvoir décider si la proposition "
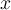est comme 
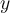" est vraie ou fausse. Ainsi, l'affirmation "
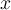" désigne le fait que appartient à la classe d'équivalence de .
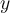Prenons comme exemple la réponse à un item de test : on considère l'ensemble des personnes à qui on soumet l'item, ainsi que l'ensemble des réponses apportées à l'item. On peut classer toute réponse selon son caractère correct ou non correct. Les réponses sont des objets empiriques en ce sens qu'on peut les observer et qu'on ne peut pas affirmer tout et n'importe quoi à leur sujet. La caractérisation des réponses du point de vue de leur caractère correct ou non correct repose sur la définition qu'on donne au terme "correct" (par exemple, "être identique à une réponse donnée"). Ainsi, on peut définir la relation d'équivalence "avoir la même réponse que" une fois que la réponse est caractérisée comme correcte ou incorrecte. On voit à travers cet exemple que le fait pour un répondant d'appartenir par sa réponse à la classe d'équivalence "correct" ou "incorrect" est le résultat d'un jugement fondé sur une définition. Ainsi, le fait d'appartenir à telle ou telle classe est un fait construit, par opposition à un fait qui s'imposerait de lui-même et en tant que tel à l'observateur.
Pour représenter l'ensemble des réponses du point de vue de cette caractérisation "correct/non correct", on peut utiliser les codes 0 pour "non correct" et 1 pour "correct". Par extension à l'ensemble des personnes, chaque personne sera ainsi échelonnée sur l'échelle (0, 1).
La classe de la personne (0 ou 1) permet de connaître le type de réponse qu'elle a fournie en traitant l'item du test, en référence à la convention qui fonde le référentiel de l'observation de la réponse à l'item.