Psychométrie : théorie et applications
Le titre développé de cette grande leçon est « Du qualitatif au quantitatif : théorie et applications ». Consacrée à la psychométrie, elle approfondit la problématique de la mesure en psychologie selon deux perspectives.
- D’une part, il s’agit d’expliciter la construction d’un observable comme le processus de composition d’applications, processus qui permet de transcrire des énoncés qualitatifs en énoncés quantitatifs.
- D’autre part, il s’agit de montrer comment l’utilisation des prévisions qu’il est possible de dériver statistiquement à partir des « sorties » de l’observation psychotechnique étaye l’intervention du psychologue dans des problématiques de dépistage, de sélection et de conseil.
1. Ordre simple
1.5. Ordre produit direct et diagramme de Hasse
On peut définir une relation binaire sur S, et la noter "
", de la manière suivante :
si et seulement si 
et 
.
Il s'agit de ce qu'on appelle la relation d'ordre produit direct.
Cette relation est une relation d'ordre, parce qu'elle permet d'ordonner par exemple les couples 11 et 23. Mais ce n'est pas une relation d'ordre simple, parce qu'elle n'est pas complète. Autrement dit, il existe des paires d'éléments de l'ensemble S que la relation "" ne permet pas de comparer. Par exemple, les éléments 12 et 21 sont incomparables.
Pour évaluer précisément l'ampleur du problème, testons la complétude forte en procédant comme dans l'exercice corrigé de la section 3. La liste ci-dessous identifie 72 cas d'incomparabilité.
Comme il existe 16×16 = 256 couples possibles, la probabilité logique d'incomparabilité est 72/256, soit environ 28%.
Pour représenter graphiquement cette relation d'ordre, on peut utiliser ce qu'on appelle un diagramme de Hasse, comme l'illustre la figure ci-dessous :
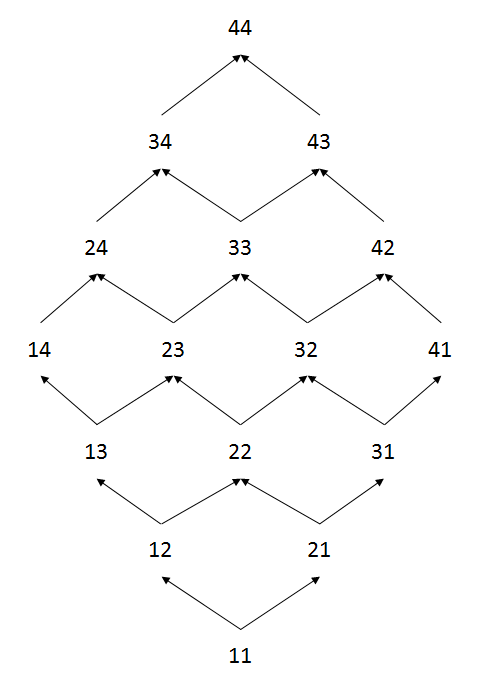
L'organisation en couches du diagramme montre que les éléments distincts d'une même couche ne sont pas comparables. Elle montre aussi que des éléments provenant de deux couches différentes ne sont pas nécessairement comparables. Par exemple, 12 et 31 ne sont pas comparables, parce que 1 > 3 et 2 < 3 (il suffit que les signes < et > soient présents quand on compare les composantes pour que les vecteurs soient incomparables). On peut aussi visualiser le concept de chaîne, c'est-à-dire de sous-ensemble qui constitue un ordre simple. Par exemple, le sous-ensemble {11, 12, 22, 32, 42, 43, 44} constitue une chaîne.