UOH / Statistique et Psychométrie en L2

1.1. Opposer ou exclure les groupes

Généralement, on réalise les comparaisons planifiées au moyen d'une analyse par contraste. Comme le nom l'indique, un contraste revient à mettre en opposition deux ensembles de données. Souvent, une troisième opération est aussi réalisée qui consiste à exclure un troisième ensemble de données.

La construction d'un contraste est la création, à partir des groupes qui opérationnalisent un facteur, d'une comparaison où l'hypothèse nulle est m₁ = m₂ . Cette création consiste à répartir les groupes en trois ensembles : (1) les groupes dont les données vont servir à construire la moyenne m₁ ; (2) ceux qui vont participer à construire la moyenne m₂ ; et enfin (3) ceux qui ne participent pas à la comparaison. 

De ce fait, la question du contraste revient à définir ce qui ira d'un côté, ce qui ira de l'autre côté, et ce qui n'allant nulle part, se trouvera exclu de la comparaison. Pour ce faire, nous définirons un contraste comme un jeu de coefficients qui affecteront chacun des groupes de l'ANOVA omnibus. Par exemple, s'il y a cinq groupes, un contraste sera un jeu de cinq coefficients.

La question devient alors de bien choisir les coefficients pour permettre la partition des groupes en trois ensembles telle qu'évoquée plus haut.

1.2. Construire le contraste

Notre problème est de construire les moyennes m₁ et m₂ à partir des moyennes des groupes de l'ANOVA. Pour cela, nous allons donc attribuer des coefficients à chacune des moyennes issues des groupes de données.

Une somme pondérée est un nombre que l'on calcule à partir d'un ensemble de valeurs auxquelles on attribue des coefficients. On fait ensuite la somme de tous les produits coefficient ×  valeur.

Si la somme de tous les coefficients en jeu dans la somme pondérée fait 1, on parlera de moyenne pondérée. Pour obtenir une somme pondérée à partir de n'importe quel jeu de coefficients dont au moins l'un est non nul, il suffit de diviser le résultat de la somme pondérée par la somme de tous les coefficients. Si en plus tous les coefficients sont égaux, nous aurons une moyenne ordinaire. Donc pour constituer les agrégats donnant m₁ et m₂, il suffira de bien choisir les coefficients.

Pour exclure un groupe, il suffira d'affecter à sa moyenne un coefficient nul.

Par ailleurs, si nous avons m₁ =m₂, cela revient à dire que m₁ - m₂ = 0, ou encore que m₂ - m₁ = 0.

En résumé, on voit donc qu'on peut facilement construire la comparaison de la façon suivante :

• Tous les groupes qui seront exclus de la comparaison recevront un coefficient nul
• Tous les groupes inclus d'un même côté de la comparaison (i.e., qui s'agrégeront pour former m₁)  recevront un coefficient positif tandis que les groupes inclus, mais qui vont de l'autre côté (i.e., qui s'agrégeront pour former m₂) recevront un coefficient négatif.

Par exemple, supposons que nous ayons 5 groupes, dont les moyennes respectives sont, faisons simple, 11, 12, 13, 14 et 15. Supposons aussi que nous voulions mettre ensemble les groupes 1 et 4, les opposer aux groupes 3 et 5, et exclure le groupe 2, nous donnerions un coefficient positif aux groupes 1 et 4, un coefficient négatif aux groupes 3 et 5, et un coefficient nul au groupe 2. Ainsi, nous pourrions choisir pour le contraste la séquence de 5 valeurs suivantes, dans laquelle la première valeur représente le coefficient du groupe 1, la deuxième valeur le coefficient du groupe 2, etc.

(1;0;-1;1;-1)

Dans ce qui suit, on expose la construction des deux termes m₁ et m₂ à des fins de compréhension de ce qu'est un contraste. En réalité, lorsque l'on teste un contraste on ne s'embête généralement pas à calculer ces moyennes : une fois qu'on a défini les coefficients, le logiciel réalise tous les calculs pour nous ! 

Pour construire l'agrégation m₁, on somme tous les produits impliquant un coefficient strictement positif (i.e., > 0)

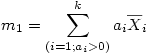
Autrement dit, nous aurons m₁ = (1×11)+(1×14)=25

Pour construire l'agrégation "- m₂", on somme tous les produits impliquant un coefficient strictement négatif (i.e., < 0).   

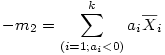
Donc, nous aurons ici -m₂ =  (-1×13)+(-1×15)  = -28, soit encore m₂ = +28.

Le signe choisi importe peu, car en réalité le contraste est la somme m ₁ + (-m ₂ ). En sommant ces deux agrégats, nous pratiquons en réalité une différence m₁-m ₂. Cette différence sera comparée à la valeur de référence 0, réalisant ainsi notre hypothèse nulle m₁ -m₂ =0 ! 

Sommer m₁ et -m₂ revient tout simplement à réécrire en une seule les deux sommes précédentes. Ce n'est même pas la peine de préciser la condition a_i ≠0 pour ne pas prendre en compte les groupes exclus de la comparaison puisque leurs coefficients étant nuls, les produits associés le seront aussi ! Nous dénoterons par la lettre Ψ le contraste ainsi obtenu et donc

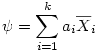
Enfin, il faut savoir que les logiciels comme SPSS ou Statistica disposent d'outils d'aide à la construction de contrastes orthogonaux comme options associées aux ANOVA.

Nous examinerons à la page suivante comment tester statistiquement cette hypothèse nulle, mais pour l'instant continuons à développer l'idée de contraste.

---

1.2. Le contraste comme généralisation de la comparaison de deux groupes

D'un certain point de vue, on peut remarquer que si l'on a k groupes, que l'on met un coefficient, disons de 1 à un groupe, de -1 à un autre groupe, et 0 à tous les autres groupes, nous nous trouvons en fait à réaliser une simple comparaison de moyennes à deux groupes, rien de plus qu'un simple test t de Student ou, ce qui revient au même une ANOVA à deux groupes. Ainsi, tester le contraste

(1;0;-1;0;0) 

revient tout simplement à faire un test de Student entre les données des groupes 1 et 3 !