UOH / Statistique et Psychométrie en L2

4.1. La question : comment rendre compte des variations expliquées par le facteur ?

Jusqu’ici, nous avons travaillé sur des contrastes élémentaires, c’est-à-dire que nous n’avons envisagé qu’un seul contraste à la fois. Mais rien qu’à partir d’un ensemble de 3 groupes, on peut construire trois comparaisons de deux groupes, et trois comparaisons opposant l’agrégation de deux des groupes au troisième. Avec quatre groupes, on peut faire des comparaisons 1 contre 3, 1 contre 2, 1 contre 1, 2 contre 2 ! Etc. les possibilités augmentent très vite avec le nombre de groupes. Et avec le nombre de comparaisons, le risque de commettre une erreur de type I quelque part (rejeter à tort l’hypothèse nulle) augmente dangereusement puisque chaque comparaison sera porteuse d’une part de risque supplémentaire.

 La question qui se pose alors est de trouver les comparaisons qui sont pertinentes d’un point de vue théorique et qui, idéalement, devraient capturer l’essentiel des variations que l’on sait expliquer, c’est-à-dire les variations représentées par la somme des carrés du facteur. On va donc chercher à trouver un ensemble de contrastes qui, à eux tous, capturent l’ensemble des variations expliquées, ni plus ni moins. 

---

4.2. Notion de comparaisons indépendantes

Pour traiter cette question, on va chercher à mobiliser des comparaisons indépendantes, de façon à ce que chaque comparaison explique des variations qui ne sont pas celles qui sont déjà expliquées par d’autres comparaisons. Deux contrastes indépendants sont dits « orthogonaux ». En effet, en géométrie, deux axes sont « orthogonaux » s’ils font un angle droit. Le fait qu’ils soient orthogonaux traduit une indépendance des coordonnées des points qui se trouvent sur l’une et l’autre puisque tout mouvement sur un axe laisse inchangé la coordonnée sur l’autre axe (monter ou descendre dans un ascenseur ne modifie aucunement ma position au sol).

On peut assimiler les contrastes à des vecteurs de k coefficients   (un coefficient par groupe du facteur). Or, en géométrie, deux vecteurs dits sont orthogonaux si la somme des produits de leurs coordonnées prises deux à deux est nulle (la coordonnée x ₁ est multipliée avec la coordonnée x₂, on y ajoute le produit de la coordonnée y₁ avec la coordonnée y₂ , etc. C’est ce que l’on appelle le produit scalaire. Donc, ici, nous dirons que :

Deux contrastes sont orthogonaux si la somme des produits de leurs coefficients est nulle.

Voici un exemple de deux contrastes orthogonaux construits avec trois groupes.  

                  (1 0 -1) et (-1 2 -1)  :  le produit scalaire donne 1*-1 + 0*2 + -1*-1 = 0

---

4.3. Ensemble de contrastes orthogonaux

Rappelons que nous voulons représenter toute la variance expliquée par le facteur. Le facteur ayant k groupes, il a k -1 degrés de liberté. Et comme un contraste n’a qu’un degré de liberté, il faudra exactement k -1 contrastes orthogonaux deux à deux pour rendre compte de l’ensemble de la variance expliquée par le facteur. 

Si l’on dispose d’un ensemble de k -1 contrastes orthogonaux, alors on a la propriété

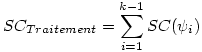
Brauer et McClelland (2005) argumentent que lorsque l’on dispose d'hypothèses a priori, plutôt que d’utiliser l’ANOVA omnibus, il faudrait travailler avec des contrastes, en s’assurant,

1. que le(s) contraste(s) cible(s) capture(nt) une part significative de la variance (ce qu’on voulait capturer est significatif)

2. que la variance intergroupe résiduelle est non significative (ce que l’on ne capture pas n’est pas important)

Concrètement, cela revient à définir le (ou les) contraste(s) cible(s) sur la base d’une analyse théorique,construire le jeu des contrastes orthogonaux supplémentaires requis pour atteindre le bon nombre de degrés de liberté (k-1 en tout), puis introduire tout cela dans une analyse globale. On peut le faire à la main, mais nous supposerons qu’un logiciel de statistiques est disponible.

On vérifie alors que les contraste(s) cibles et eux seuls sont significatifs.