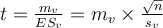UOH / Statistique et Psychométrie en L2

A. Dans quel cas appliquer un tel test ?

Objectif.  Le test du t de Student s'applique lorsque l'objectif est soit de comparer deux moyennes entre elles, soit de comparer une moyenne contre une constante.

Type des informations disponibles : Les valeurs mesurées doivent être numériques, faute de quoi l'idée même de moyenne n'a pas de sens.

Distribution des observations : Les données doivent être normalement distribuées : l'histogramme doit être symétrique et ressembler peu ou prou à une courbe en cloche. On peut aussi appliquer des tests formels de normalité.

Condition d'indépendance : Les données doivent être indépendantes (les données d'un sujet ne sont pas censées avoir influencé les mesures faites sur un autre sujet).

B. Qu'est-ce que la statistique t ?

B.1 Rappel sur la loi normale centrée réduite

Vous trouverez dans le cours de L1 une présentation simple de la loi normale centrée réduite, accompagnée d'un générateur de simulations pour que vous puissiez faire des tests : Cliquez ici pour y accéder.

B.2 Notions d'échantillons virtuels et réels.

Avertissement : Ces deux notions sont propres au présent cours et vous ne les trouverez sans doute nulle part ailleurs. Nous les introduisons afin de permettre une vue générale du test t.

Nous appelons ici échantillon réel un ensemble de mesures directement réalisées sur une population. Par exemple, une mesure d'intelligence prise sur un ensemble de participants à une étude.

Nous appelons échantillon virtuel l'échantillon des données composé à partir des éléments à comparer. Ces éléments peuvent être (1) un échantillon réel et une constante (cas de la comparaison d'une moyenne à une constante); (2) deux échantillons réels de mesures indépendantes (c.-à.d. des mesures prises sur des individus différents et qui ne se sont pas influencés par ailleurs); (3) deux échantillons réels de mesures appariées (c.-à.d. des paires de mesures prises pour chaque individu, où la première mesure va dans l'échantillon réel 1 tandis que la seconde mesure va dans l'échantillon réel 2).

B.3 Formule générale de la statistique t.

Dans toutes les formes du test de Student, la statistique calculée se nomme " t ". Soient m_v la moyenne d'un échantillon virtuel de taille n_v et ES _v son erreur-standard (on rappelle que l'erreur standard d'un échantillon s'obtient en divisant l'écart-type par la racine carrée de l'effectif), on a

$t=\frac{m_v}{ES_v}=m_v\times\frac{\sqrt{n}}{s_v}$

Cette formule s'applique dans le cas des trois tests t considérés dans cet article, test t pour échantillon unique, pour échantillons appariés et pour échantillons indépendants. Comment est-ce possible ? Tout simplement parce que l'échantillon auquel nous faisons référence ici est un échantillon virtuel que nous construirons différemment dans les trois cas. Nous verrons comment plus loin mais, pour l'instant, continuons l'analyse sur cet échantillon virtuel.

Pourquoi utiliser cette note t plutôt que simplement une valeur centrée-réduite z dont la distribution est connue puisque c'est celle de la loi normale centrée-réduite ? Eh bien, pour la raison suivante, qui se comprend par un raisonnement en deux points.

• Parce que si la moyenne m_v et l'écart-type s_v de l'échantillon peuvent être considérés comme des estimateurs des paramètres "réels" de la population d'où est tiré l'échantillon, à savoir sa moyenne μ et son écart-type σ, ces estimateurs ne sont pas l'exacte réalité mais seulement une approximation de la réalité.
• Si cette approximation de la moyenne μ par m peut être considérée comme fiable (au sens où si l'on tirait un nombre infini d'échantillons, la moyenne des moyennes issues de tous ces tirages convergerait vers la "vraie" moyenne, celle de la population), ce n'est pas le cas pour l'écart-type s . En effet, ce dernier est biaisé de façon systématique par rapport à l'écart-type σ de la population d'où est extrait l'échantillon, et la taille du biais dépend de la taille des échantillons que l'on prend : plus l'échantillon est petit et plus le biais est important. Il nous faut donc une loi qui corrige ce biais. Comme ce biais dépend de la taille des échantillons, il faut que cette loi admette un paramètre qui représente cette taille alors que la loi normale centrée-réduite ne dépend pas du tout de l'effectif.

Mais alors, si l'on ne peut pas utiliser la loi normale... 

C. Comment obtenir la valeur p associée ?

C.1. La loi du t

La variable t suit elle-même une loi ou distribution, dite loi du t de Student que l'on a présentée dans le cours de première année. Simplement, on peut considérer que les valeurs de t constituent une loi normale aménagée pour corriger le biais induit par la petite taille de l'échantillon. Plus l'échantillon est grand et moins il y a de biais à corriger et donc plus la loi du t ressemble à la loi normale.

La loi normale dépend de la moyenne et de l'écart-type, mais dans la loi centrée-réduite, ces deux paramètres sont fixés à 0 et 1 de sorte que la loi normale centrée-réduite est entièrement déterminée. La loi du t en est une sorte d'adaptation. Elle dépend d'un paramètre supplémentaire, le nombre de degrés de liberté, qui traduit l'ampleur de la correction qu'il faut apporter. Si l'on connaît le nombre de degrés de liberté, on peut alors déduire les valeurs p associées exactement selon les mêmes principes que l'on a utilisés pour la loi normale centrée réduite.

Il existe des tables du t que l'on peut utiliser lorsque l'on n'a pas de logiciel, mais on trouve maintenant des logiciels gratuits, à commencer par le tableau de la suite OpenOffice, permettant de calculer les valeurs de p associées à t avec précision. Vous trouverez ici des vidéos de démonstration du calcul du test de student. 

C.2. Unilatéral ou bilatéral ?

Comme la distribution du z, la distribution du t est symétrique autour de 0. Par conséquent, si l'on possède une hypothèse théorique précisant le sens de la différence attendue des moyennes que l'on compare (par exemple, on s'attend à ce que la taille moyenne des garçons soit supérieure à la taille moyenne des filles d'une même classe d'âge) ET que les résultats vont dans le sens attendu, alors on peut diviser la valeur p que donnait le test bilatéral par deux. Ainsi, pour 50 degrés de liberté une valeur de t =1.69 est associée à une valeur p de 0.0972. C'est supérieur au seuil conventionnel de 5% et donc on dira que ce n'est pas significatif (on pourra cependant parler de "tendance" car la valeur p est comprise entre .05 et .10.

Si l'on peut travailler en unilatéral, on divise cette valeur par 2, ce qui donne p =.049, ce qui cette fois est significatif. Bien évidemment, lorsque vous rapportez vos résultats, il faut préciser que la valeur a été calculée en unilatéral.

D. Comment présenter les résultats d'un test t ?

Nous nous basons ici sur les normes internationales en vigueur en psychologie, les normes de l'APA (American Psychological Association), 7^e édition.

D.1. Les statistiques descriptives

Le test du t est avant tout une comparaison de moyennes, comparaison qui repose sur une ou des mesures de dispersion. Il faut donc impérativement rapporter les données de statistiques descriptives, y compris la dispersion. Les débutants ont souvent tendance à l'oublier, tout à la joie de pouvoir rapporter un résultat "significatif", mais les statistiques inférentielles ne sont que des informations de second ordre, des indicateurs sur la fiabilité des résultats obtenus. Les informations de premier ordre, celles qui disent ce que l'on a vraiment observé, ce sont les statistiques descriptives et non les statistiques inférentielles !

Ces statistiques descriptives peuvent être présentées dans le texte du compte-rendu ou bien, le plus souvent, dans une table.

Lorsque l'on compare des groupes de tailles différentes, il est courant de donner comme indice de dispersion non pas la variance ou l'écart-type, qui sont très sensibles à la taille de l'échantillon, mais l'erreur standard qui l'est moins. On l'a dit plus haut, l'erreur standard s'obtient en divisant l'écart-type par la racine carrée de la taille de l'échantillon. Par exemple, si l'écart-type vaut 3.0 et qu'il y a 20 sujets, cela fait une erreur standard de 3/racine(20) = 0.67. 

D.2. Les statistiques inférentielles.

Comme la distribution du t dépend du nombre de degrés de liberté, il convient de préciser celui-ci lorsque vous rapportez vos résultats. Cela donne une structure de la forme suivante :

                                                               t (ddl)=n.nn, p =.xxx

• ddl est le nombre de degrés de liberté. Dans un test t, c'est le nombre de sujets de l'échantillon virtuel diminué de 1. Nous verrons dans chacun des trois cas de test t comment calculer ce nombre.
• La valeur n.nn peut se rapporter avec un signe ou non mais, en tout cas, il est inutile de rapporter plus de deux décimales. Les logiciels donnent souvent des valeurs signées et avec plus de deux décimales, mais en pratique le signe du t est sans importance, et donner plus de deux décimales est foncièrement inutile.

Enfin, la façon de rapporter les valeurs de p est tout à fait conventionnelle et ne dépend pas du type de test utilisé ¹ . 

¹. Selon les normes de publication en vigueur en psychologie scientifique, il est maintenant d'usage de rapporter, outre les valeurs de t et le p associé, une variable représentant ce qu'on appelle la "taille d'effet". Le calcul manuel de cette dernière n'est pas encore intégré dans la présente version de ce cours. Le calcul par logiciel des tailles d'effets est toutefois présenté dans les vidéos de savoir-faire sur les comparaisons de moyennes.