Statistique : comparer des moyennes
Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
3. Comparer plus de deux moyennes : L'ANOVA à un facteur
3.6. Calculer la somme des carrés totale
Imaginons que nous fassions une ANOVA où l'effet du facteur G est étudié au travers de mesures prises sur k groupes, dont les effectifs sont respectivement n1, n2, ... , nk . Soit un effectif global N = n1 + n2 +...+ nk.
Il s'agit de capturer l'ensemble de toutes les variations, c'est-à-dire l'ensemble des variations de toutes les mesures de tous les groupes. S'il n'y avait aucune variation, L'échantillon global (composé des échantillons issus de chaque groupe) aurait exactement la valeur globale de la population étudiée, et donc la moyenne de l'échantillon global serait égale à la moyenne générale de la population. De plus, toujours dans ce monde hypothétique, chacun des différents groupes aurait la même moyenne que la moyenne de l'ensemble de tous les groupes.
Donc pour calculer la variance associée aux variations totales, il faut calculer les écarts à la moyenne générale de toutes les mesures ("Grand Mean" en anglais), quel que soit le groupe d'où proviennent les mesures.
Et la somme des carrés totale est donc tout simplement liée à la variance totale de toutes les mesures de la VD.
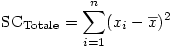
Le nombre de degrés de liberté associés à cette somme de carrés est le nombre total de sujets - 1 :
ddlTotal = N - 1
Le CM totale s'obtient en divisant la SC Totale par le ddl Total.
CMTotal = SC Total / ddl Total
Voyons un exemple numérique sur des données fictives :
La colonne X contient les notes de chaque élève, quel que soit leur groupe. Le total de toutes ces notes est 167. Il y a 16 notes, donc la moyenne générale (Grand Mean en anglais) est 167/16 = 10.4375
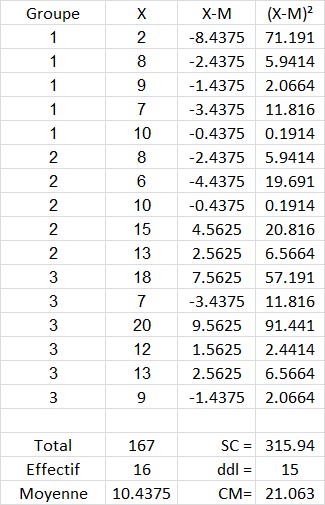
Pour chacune de ces notes, on place dans la colonne intitulée ici X-M l'écart entre la note et la moyenne générale, puis dans la colonne suivante, nommée " (X-M)² ", on passe cet écart au carré. Bien sûr, on aurait pu tout mettre en une seule formule, mais il s'agit ici d'illustrer le détail du calcul.
La somme de cette dernière colonne est la somme des carrés totale, soit 315.9375, arrondie sur l'image à 315.94.
Le nombre de degrés de liberté est l'effectif total - 1, soit 15.
Le carré moyen s'obtient en divisant l'un par l'autre, soit 315.9375/15 = 21.063.
Vous pouvez vérifier aisément au moyen d'une formule de tableur que ce carré moyen est directement donné par la variance de l'échantillon des 16 mesures.