Statistique : comparer des moyennes
Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
3. Comparer plus de deux moyennes : L'ANOVA à un facteur
3.7. Calculer la somme des carrés inter-groupes (SC du facteur)
Dans une ANOVA, le "facteur" (aussi appelé "traitement") correspond à la répartition des sujets en différents groupes expérimentaux. "L'effet du facteur" résidera donc dans le fait que les groupes auront des moyennes plus ou moins différentes.
Pour comprendre l'analyse qui sera faite, il faut savoir que si l'on considère la réponse d'un sujet donné, on peut considérer qu'une partie de son score est due au fait que c'est un sujet issu de la population générale, qu'une autre partie est due au fait qu'il appartient à tel groupe, et enfin qu'une dernière partie résulte de facteurs aléatoires qu'on ne connaît pas. S'il n'y avait pas de variation aléatoire, tous les sujets d'un même groupe auraient produit la même valeur. Et cette valeur serait la moyenne du groupe. De ce fait, l'effet du facteur est l'écart entre la moyenne du groupe et la moyenne générale.
Pour l'analyse en termes de sommes des carrés, il faut donc remplacer la mesure de chaque individu du groupe par la valeur moyenne du groupe. Puis calculer la somme des carrés de la même façon que la somme des carrés totale.
6.1. Approche intuitive
Reprenons l'exemple numérique vu dans le calcul de la SC Totale :
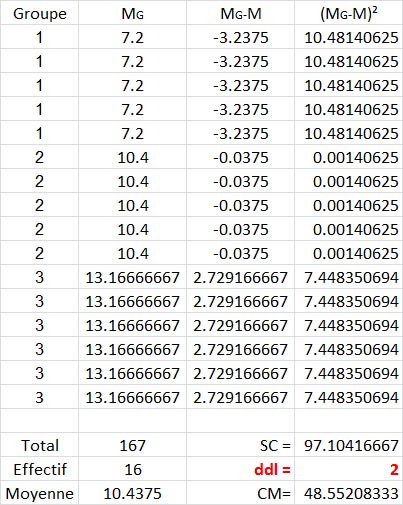
Vous voyez qu'on a remplacé chaque valeur individuelle (l'ancienne colonne "X") par la valeur de la moyenne du groupe (Colonne "M G "), par exemple, 7.2 pour les données du groupe 1). La moyenne générale M est ensuite retirée de la moyenne du groupe (Colonne "MG - M") pour chaque individu et le tout passé au carré selon le même principe que pour la somme des carrés totale (Colonne "(MG - M)²"). La somme de tous ces écarts carrés est la SCInter soit ici 97.10416667.
Attention !! Le nombre de degrés de liberté en revanche n'est pas (16 - 1) mais (3 groupes - 1), soit 2 (en rouge sur l'image) !! Du coup le carré moyen est la somme des carrés divisée par 2 et non par 15 !!
6.2. Approche formelle
Pour les étudiants désireux d'une approche plus formelle, voici des formules qui exposent la démarche. En notant la moyenne générale des N sujets
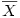
et en notant la moyenne du k ième groupe (c'est-à-dire du groupe Gk)
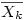
on aura alors pour les nk individus du groupe k la somme des carrés suivante :
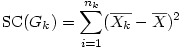
ou, ce qui revient au même,
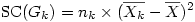
Vous noterez que cette formule ne préjuge pas de l'équilibre des effectifs, c'est-à-dire que si des groupes ont des tailles différentes, la somme des carrés d'un groupe sera proportionnelle à son effectif.
Finalement, on somme les SC de chacun des groupes pour obtenir la somme des carrés du facteur :
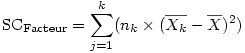
Le nombre de degrés de liberté associés à cette somme de carrés est le nombre de groupes - 1. Donc si l'on suppose un facteur à k groupes, on a
ddlFacteur = ddl Inter = k - 1