UOH / Statistique et Psychométrie en L2

7.1. Option simple : par différence

Il suffit de faire la différence des deux précédentes sommes de carrés :

SC_Intra = SC_totale - SC_Inter

Le nombre de degrés de liberté associés peut lui aussi s'obtenir en faisant la différence entre le nombre de degrés de liberté de la SC_Totale et le nombre de degrés de liberté de la SC_Inter.  Soit,  

  ddl_Intra = ddl_Total - ddl_Inter = (N - 1) - (k - 1),

Et donc  finalement

ddl_Intra =  N - k

Sur l'exemple, vous pouvez vérifier facilement que la SC_intra est la différence des deux autres, et qu'il en va de même pour les ddl_intra. Bien sûr, le CM ne peut se calculer aussi par différence, il faut rediviser la SC_Intra par les ddl_Intra.

---

7.2. Option complexe : directement

On peut aussi calculer les choses directement, si vous voulez vérifier les calculs par exemple.

Pour ce faire, on considère chaque groupe comme s'il était complètement indépendant des autres. On calcule la somme des carrés exactement de la même façon que la somme des carrés totale, mais en appliquant la formule aux seules données du groupe. Il suffit ensuite de sommer les SC obtenues indépendamment sur chacun des groupes pour avoir la SC_Inter.

Chaque groupe est alors associé à un nombre de degrés égal à son effectif  - 1, soit N_k - 1 et le nombre de degrés de liberté associés à la SC_Intra s'obtient en faisant la somme des k groupes, ce qui donne N₁ - 1 + N₂ - 1 +... + N_k - 1, soit encore N₁ + N₂ + ... + N_k - 1 - 1 -... - 1 (on enlèvera k fois 1, donc au total, k), et donc puisque N₁  + N₂ + ... + N_k = N, on obtient bien ddl_Inter = N - k.

Reprenons notre exemple numérique :

Pour le groupe 1 nous avons :

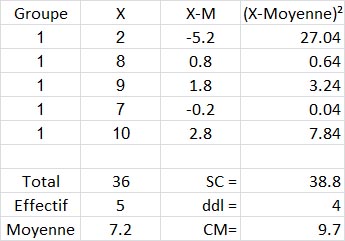
Pour le groupe 2 nous avons :

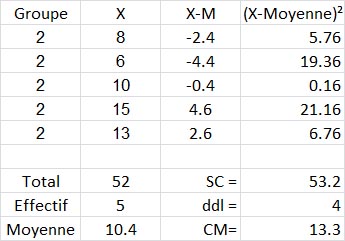
Pour le groupe 3 nous avons : 

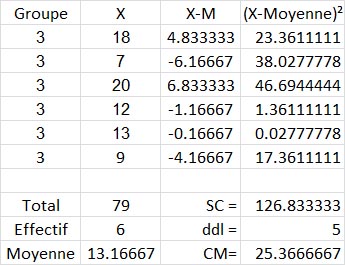
Et, finalement, nous faisons la somme des SC issues des trois tableaux précédents, nous trouvons SC_Intra =38.8+53.2+126.83, soit 218.83. 

Et pour les ddl_Intra , nous avons bien 4+4+5=13.