UOH / Statistique et Psychométrie en L2

Les méthodes de test sont proposées ici par ordre du plus laxiste au plus conservateur.

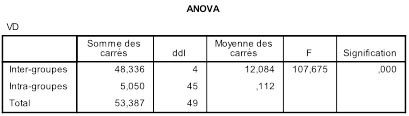
Bien entendu, nous avons commencé par réaliser une ANOVA à un facteur sur ces données. Il se trouve que l'ANOVA globale est largement significative mais ce n'est pas une nécessité pour tous les tests que nous allons voir :

3.1    Le test de la plus petite différence significative (LSD) de Fisher

3.1.1. Idée générale du test

Le plus laxiste des tests post-hoc est le test de Fisher dit LSD (pour Least Square différence).

La « différence des moindres carrés » est en fait tout simplement la différence des moyennes des deux groupes, comme dans n’importe quel test t. De fait, ce test consiste à calculer un t de Student. Rappelons que ce dernier consiste basiquement à diviser une différence de moyennes par l’erreur standard de l’échantillon virtuel composé des deux groupes à comparer (voir l’article ici).

L’idée du test LSD de Fisher est de réaliser un test t de la même façon que d’habitude, mais avec un niveau de bruit qui n’est pas limité aux variations internes aux deux groupes cibles. Au contraire, il intégrera l’ensemble des bruits de tous les groupes. Pour ce faire, on prendra à la place de l’erreur standard de l’échantillon virtuel (celui construit par agrégation des deux échantillons à comparer) la racine carrée du carré moyen de l’erreur dans l’ANOVA.

L’erreur standard, rappelons-le, n’est autre qu’une sorte d’écart-type normalisé par la taille de l’échantillon, puisqu’il s’agit de la racine carrée de la variance divisée par la racine carrée de l’effectif. Mais cette normalisation est ici limitée par le fait qu’on la calcule en calculant l’écart-type à partir de l’effectif de l’échantillon virtuel (la somme des effectifs des deux groupes) et non à partir de l’effectif global qui a servi à générer la mesure des variations !

Si n est le nombre total de sujets (50 dans l'exemple), et k le nombre de groupes (5 dans l'exemple), M_i et M_j les moyennes de deux groupes à comparer de manière post-hoc, beaucoup de ces tests font usage d’un calcul du test t de Student, avec n-k degrés de libertés calculé par la formule suivante pour groupes équilibrés (les groupes sont de tailles égales, ce qui est le cas ici) :

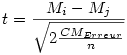
Nous pouvons repérer directement le CM_Erreur dans le tableau d'ANOVA à la ligne intra-groupes : 0,112. Attention, il sera utilisé pour la plupart des tests post-hoc que nous verrons.

3.1.2. Application numérique

Voici les résultats que donne SPSS sur notre exemple : 

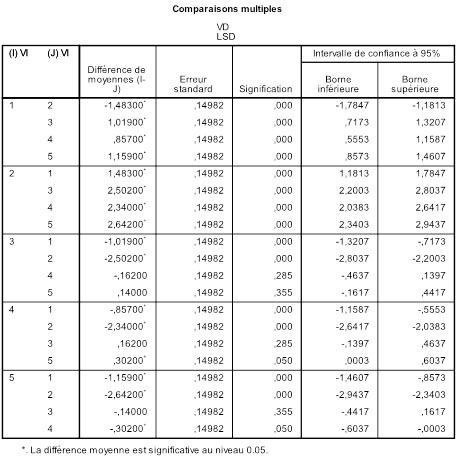
Vous voyez que toutes les comparaisons par paires possibles sont explorées. Si nous prenons par exemple le sous-tableau des comparaisons impliquant la moyenne M₁, nous voyons qu'il y a une ligne par moyenne comparée avec M₁. La première ligne compare M₁ et M_2.

Pour notre exemple, nous prendrons i =1 et j =2. La différence des moyennes est (voir le tableau des moyennes par groupes à la page précédente)

M₁ - M_2.  = 1.536 - 3.019 = -1.483

Le t s'obtient en divisant la différence des moyennes par l'erreur standard intra-groupes, laquelle s'obtient dans le cas présent (groupes équilibrés, variances homogènes) par la formule suivante :

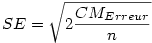
où n est le nombre de sujets par groupe. Ce qui donne

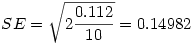
Vous remarquerez que l'erreur standard ne change pas quelle que soit la paire de groupes que l'on considère. C'est normal puisqu'on la calcule une fois pour toutes sur la base du carré moyen de l'erreur dans l'ANOVA. Par contre, le t change avec les paires. Ici, on a t =-1.483/0.14982 = -9.899. Cette valeur est largement significative, au point que la valeur p présentée dans le tableau de résultats, quoique non nulle, est tronquée à p=.000.

Le t que nous venons de calculer ne figure pas explicitement dans le tableau. Nous pouvons néanmoins utiliser la ligne 4 du sous groupe 3 qui, n'étant pas significative, nous donne une valeur p plus exploitable pour vérifier nos formules. L'erreur standard est la même et la différence de moyenne est -.162. D'où un t =-.162/0.14982=-1.081. Nous testons cette valeur t avec N - k =50-5=45 degrés de libertés. En utilisant une formule de tableur (Sous Excel par exemple "=LOI.STUDENT.BILATERALE(ABS( t ); ddl )", en remplaçant t par sa valeur et ddl par 45), et après arrondi, nous obtenons effectivement la valeur p =.2853.

Bien entendu, le test est bilatéral puisque post-hoc et que donc nous n'avions pas d'hypothèse. Notez dans la formule la fonction "abs", valeur absolue, rendue obligatoire par le fait que le t peut être de signe négatif, ce qui est d'ailleurs le cas ici.

3.1.3 Pourquoi le LSD est-il "laxiste" ?

Tout simplement parce que les valeurs p sont calculées exactement comme d’habitude, sans véritable protection contre l'augmentation du risque au niveau de l'ensemble des comparaisons ! La conséquence est que le taux d’erreur de l’ensemble va tendre à excéder le seuil de .05, et ce d’autant plus qu’on a de groupes en jeu. Selon Howell, et pour des raisons qui seraient trop complexes à développer ici, il existe tout de même un cas où il est légitime, et même recommandé :
•    Si l’ANOVA globale est significative ET
•    s’il n’y a que trois groupes en jeu.

Dans les autres configurations, ce test est à éviter.

3.2    Le test Student-Newman-Keuls

Le test Student de Newman-Keuls s’appuie sur la statistique q dite « statistique d’écart studentisée » qui s’obtient sur la base d’un classement des moyennes comparées de la plus petite à la plus grande. On lit la significativité de q à partir d’une distribution d’échantillonnage (ou on compare q aux valeurs critiques données par une table de la statistique q) avec pour paramètres le nombre r d’échelons d’écart entre les groupes comparés (pour en savoir plus, voir l’article spécifique) et le nombre de degrés de libertés de l’erreur dans l’ANOVA.

Par exemple, s’il y a cinq groupes, et qu’après rangement des moyennes M₁, la plus petite, à M₅, la plus grande, et qu’on compare M₃ et M₄, on prendra r =1 pour entrer dans la table de q.
Quoiqu'encore utilisé, ce test est maintenant de plus en plus déconseillé, car le risque de commettre au moins une erreur au niveau de l’ensemble des comparaisons augmente presque linéairement avec le nombre de paires de moyennes à comparer.

3.3    Le test de la différence vraiment significative de Tukey

Le test HSD de Tukey, test de la différence vraiment significative (HSD signifie « Honestly Significant difference ») s’appuie comme le précédent sur la statistique d’écart studentisée q.

Pour le test HSD de Tukey, toutefois, on fait comme si TOUTES les comparaisons avaient le nombre maximum d’échelons possibles. Ainsi, même si l’on compare les moyennes M₃ et M₄ parmi 6, on calculera la significativité de q à partir de r =6 et non à partir de r =2.

Contrairement au LSD, qui est trop laxiste, le HSD est conservateur puisqu’il traite tous les cas comme si c’était le pire.

Le test HSD teste l’hypothèse nulle globale et suppose que les données soient normalement distribuées.

Pour le détail du calcul de q, nous renvoyons à l’article correspondant.

Voici les résultats que donne SPSS pour nos données :

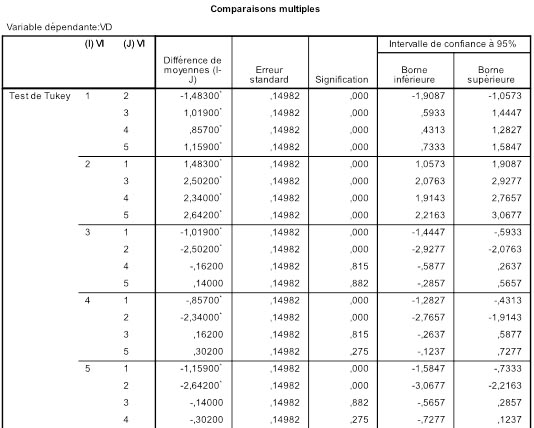
En regardant la ligne 4 du groupe 3, on voit immédiatement que le test de Tukey est plus conservateur que le LSD puisque la valeur p obtenue est .815 alors que le LSD donnait .2853 ! L'erreur standard et la différence de moyenne étant les mêmes, c'est au niveau des paramètres de la statistique q que va se faire la différence. En effet, la distribution d'échantillonnage de q admet deux paramètres, le nombre de degrés de libertés, qui ne change pas ici, et la taille de l'écart. Dans le cas présent, variances homogènes et effectifs équilibrés, nous pouvons obtenir q facilement à partir de t puisque dans ce cas

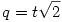
Puisque nous avons déjà calculé t plus haut (voir test LSD), on obtient donc q =-1.5292.

On entre alors dans une table de q avec 45 degrés de liberté et r =5 ou bien nous prenons un logiciel comme R dont la commande "ptukey" nous donne les valeurs p associées à la distribution d'échantillonnage de q (commande : "ptukey(1.5292,5,df=45,lower.tail = FALSE)", et nous trouvons p =0.815123, conformément au résultat présenté dans la table SPSS.

Bien sûr, on aurait pu aussi procéder en comparant le q observé q_obs aux valeurs critiques d'une table. Ainsi avec r =5 et ddl =45 degrés de liberté, on lit la valeur critique au seuil α=.05, notée q _.05 (5,45). On trouve q _.05 (5,45)=4.018. Puisque q_obs =1.529<q _.05 (5,45), on sait que le test n'est pas significatif.

Attention : Dans les cas où les effectifs sont déséquilibrés ou encore lorsque les variances sont hétérogènes, voire les deux, il faut adapter le calcul de q_obs selon les corrections présentées ici ).

À noter : SPSS offre une variante du HSD, dite « B de Tukey », dans laquelle la valeur critique de q est obtenue par moyennage entre la valeur critique donnée par le HSD et celle obtenue par le Student-Newman-Keuls.

3.4    La procédures REGW test Q et test F

REGW signifie Ryan-Einot-Gabriel-Welsch du nom des contributeurs successifs à l’élaboration de la procédure. Il s’agit donc d’une procédure qui utilise soit q, la statistique d’écart studentisée, soit un test F. Selon Howell, lorsqu'on dispose d'un logiciel pour la calculer, cette approche représente le meilleur compromis entre la nécessité de limiter l’erreur de l’ensemble des comparaisons et la nécessité de garder une puissance statistique suffisante pour rejeter l’hypothèse nulle si besoin est.

Pour réaliser ce compromis, le REGW ajuste les seuils critiques en utilisant non pas le 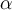$\alpha$ de la comparaison globale, mais un 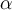$\alpha$_r qui s’obtient par une formule qui requiert l’automatisation qu’offrent seulement certains logiciels de statistique (dont notamment R via le package regwq, et SPSS).